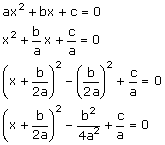
Klaar! Want de top is dan
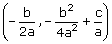 .
.Zie ook Wat is kwadraatafsplitsen? en De co÷rdinaten van de top berekenen.
WvR
5-12-2005
Hoe kan je door middel van kwadraatafsplitsen van ax2+bx+c komen tot de formule om de top van een parabool te berekenen (-b/2a?
Ik weet al hoe je bij de ABC-formule het kwadraat kan afsplitsen. Namelijk:
ax2+bx+c=0
4a2x2+4abx+4ac=0
4a2x2+4abx+b2=b2-4ac
(2ax+b)2=b2-4ac
2ax+b=▒Íb2-4ac
x=-b▒Íb2-4ac/2a
Ook weet ik dat je voor de formule om de x-co÷rdinaten van de top te berekenen er dus alleen voor moet zorgen dat je b2-4ac 'kwijtraakt'. Maar hoe doe je dit. Je mag ze toch niet zomaar weglaten?Arne van Bonzel
5-12-2005
Klaar! Want de top is dan.
Zie ook Wat is kwadraatafsplitsen? en De co÷rdinaten van de top berekenen.
WvR
5-12-2005
#42029 - Functies en grafieken - Leerling bovenbouw havo-vwo