|
|
|
\require{AMSmath}
Een goed te begrijpen bewijs voor de volgende stelling
Weet iemand een goed te begrijpen bewijs voor de stelling: De oppervlakte van een driehoek met zijden a, b en c is gelijk aan √(s(s-a)(s-b)(s-c)) waarbij s=1/2(a+b+c).
Gerard
Leerling onderbouw vmbo-havo-vwo - zaterdag 21 mei 2005
Antwoord
Hallo Gerard,
Het bewijs moet sluitend zijn voor alle driehoeken, dus ik ga uit van onderstaande willekeurige driehoek. Zonder rechte hoek dus.
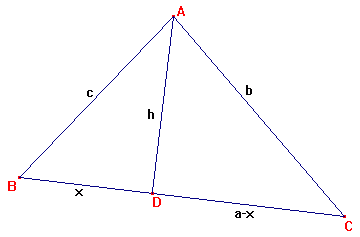
We zien 2 Pythagoras driehoeken: ABD en ADC.
Hierbij horen de vergelijkingen: c2=h2+x2 en b2=h2+(a-x)2
Ofwel: h2=c2-x2 en h2=b2-(a-x)2
Hieruit volgt: c2-x2=b2-(a-x)2 Zo ook: c2−x2=b2−(a2− 2ax+x2)
En: c2−x2=b2−a2+2ax−x2 En: c2=b2−a2+2ax
Dus: 2ax=a2−b2+c2
Conclusie: x=a2−b2+c2/2a
Deze x nu invullen in: h2=c2-x2=(c - x)(c + x)
Dit levert: h2=(−a+b+c)(a+b−c)(a−b+c)(a+b+c)/4a2
Nu komt de s erbij, om bovenstaande vergelijking te vereenvoudigen. De nieuwe letter s staat voor de halve omtrek, dus 1/2(a+b+c).
We krijgen nu de volgende vergelijkingen:
(a+b+c)=2s
(-a+b+c)=2s-2a
(a+b-c)=2s-2c
(a-b+c)=2s-2b
De eerder gevonden formule: h2=(−a+b+c)(a+b−c)(a−b+c)(a+b+c)/4a2 gaat dus nu over in:
h2=2s(2s−2a)(2s−2b)(2s−2c)/4a2
Dus: h2=4s(s-a)(s-b)(s-c)/a2
Dus: h=2√s(s-a)(s-b)(s-c)/a
En omdat (kijkend naar het beginplaatje) de oppervlakte van de driehoek ah/2 is, is nu de oppervlakte van de driehoek dus ook:
√s(s-a)(s-b)(s-c)
Zo kun je dus de oppervlakte van elke willekeurige driehoek berekenen als de de drie zijden weet.
Duidelijk Gerard?
Groeten, FV
Zie De formule van Heron
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 mei 2005
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Een goed te begrijpen bewijs voor de volgende stelling