|
|
|
\require{AMSmath}



Meetkunde van de driehoek
ik heb een opdracht gekregen om een bewijs te zoeken maar kan niks vinden.
ik moet bewijzen dat de oppervlakte van een driehoek met zijden a, b, c gelijk is aan de wortel van sx(s-a)x(s-b)x(s-c) waarbij s = 1/2x(a+b+c)
ik hoop dat jullie mij hierbij kunnen helpen.
dyon b
Leerling onderbouw vmbo-havo-vwo - dinsdag 10 mei 2005
Antwoord
als je s*(s-a)*(s-b)*(s-c) uitwerkt krijg je:
1/16*(2a2b2+2a2c2+2b2c2-a4-b4-c4) (ga dat zelf na).
Bekijk nu onderstaande tekening:
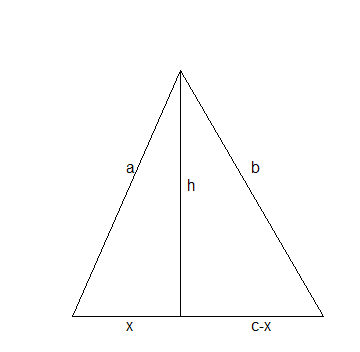
Voor de hoogtelijn h krijgen we:
h2=a2-x2=b2-(c-x)2
Er geldt dus
a2-x2=b2-c2+2cx-x2
Hieruit volgt:
x=(a2+c2-b2)/(2c) (ga na)
Dus h2=a2-x2=a2-(a2+c2-b2)2/(4c2)
Het kwadraat van de oppervlakte is 1/4h2*c2=
1/4a2c2-1/16(a2+c2-b2)2
Als je deze uitdrukking vereenvoudigt krijg je weer:
1/16*(2a2b2+2a2c2+2b2c2-a4-b4-c4).
(Ga dat zelf na)
Ga nu na dat het bewijs is geleverd.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 11 mei 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










