WisFaq!

Meetkunde van de driehoek

ik heb een opdracht gekregen om een bewijs te zoeken maar kan niks vinden.
ik moet bewijzen dat de oppervlakte van een driehoek met zijden a, b, c gelijk is aan de wortel van sx(s-a)x(s-b)x(s-c) waarbij s = 1/2x(a+b+c)
ik hoop dat jullie mij hierbij kunnen helpen.

dyon beuken
10-5-2005

Antwoord

als je s*(s-a)*(s-b)*(s-c) uitwerkt krijg je:
1/16*(2a²b²+2a²c²+2b²c²-a⁴-b⁴-c⁴) (ga dat zelf na).

Bekijk nu onderstaande tekening:


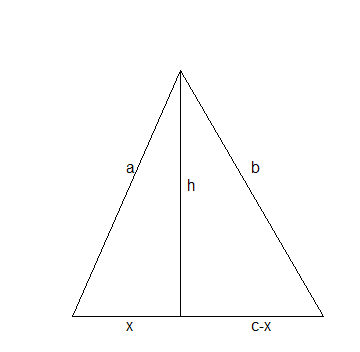
Voor de hoogtelijn h krijgen we:
h²=a²-x²=b²-(c-x)²
Er geldt dus
a²-x²=b²-c²+2cx-x²
Hieruit volgt:
x=(a²+c²-b²)/(2c) (ga na)
Dus h²=a²-x²=a²-(a²+c²-b²)²/(4c²)
Het kwadraat van de oppervlakte is ¹/₄h²*c²=
¹/₄a²c²-¹/₁₆(a²+c²-b²)²
Als je deze uitdrukking vereenvoudigt krijg je weer:
1/16*(2a²b²+2a²c²+2b²c²-a⁴-b⁴-c⁴).
(Ga dat zelf na)
Ga nu na dat het bewijs is geleverd.

hk
11-5-2005