WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vierhoek berekenen

Dit is een reactie op vraag 32945

Hallo,

heb net antwoord gekregen, maar ik kom er niet uit.

Gegeven :
- vierhoek abcd
- ab = 30,45
- bc = 30,55
- cd = 30,55
- da = 30,45
ab is evenwijdig aan cd

Gevraagd : bereken ac en bd.

Dank

Dirk

Dirk
Iets anders - donderdag 20 januari 2005

Antwoord

dag Dirk,

Dan maar even een tekening als hulpmiddel.

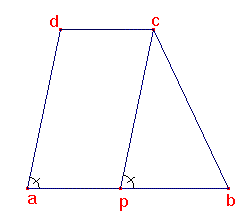
In mijn tekening is ab langer dan cd, maar dat maakt voor het principe niet uit. Desnoods hernoem je de punten.
Nu zijn de drie zijden van driehoek pbc bekend.
Daarmee heb je de mogelijkheid om Ðcpb te berekenen met de cosinusregel. Noem deze hoek a:
bc² = pb² + pc² - 2·pb·pc·cos(a)
waaruit cos(a) te berekenen is.
Maar Ðdab is ook gelijk aan a.
Dus er geldt in Dabd:
bd² = ab² + ad² - 2·ab·ad·cos(a)
waarmee je dus de diagonaal bd kunt uitrekenen.
Overigens is jouw vierhoek tamelijk vierkant, waardoor je al een behoorlijk goede benadering van de lengtes van de diagonalen kunt krijgen door de zijde te vermenigvuldigen met Ö2.
NB. als de vier zijden echt precies even lang zijn, dan kun je de diagonalen niet berekenen, omdat je dan oneindig veel mogelijkheden hebt: allemaal ruiten die meer of minder platgedrukt kunnen worden.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 20 januari 2005