WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelling van Desargues

Het probleem is de hele stelling. Figuur 18a van http://www.pandd.demon.nl/transvers.htm
volgens de stelling van Menelaos zijn de punten collineair als (ABP)(BCQ)(CAR),
maar als ik me niet vergis lees je het zo dat: de lijn AB het snijpunt P met de transversaal opleverd.
maar bij de stelling van desargues zeggen ze dat BC het punt P met de transversaal opleverd.
beetje tegenstrijdig?
hoe zit dit
bij voorbaat bedankt
wilco
Leerling bovenbouw havo-vwo - donderdag 16 december 2004

Antwoord

Op de bedoelde pagina is de tekst bij het plaatje onjuist (of eigenlijk: er staat een verkeerd plaatje).

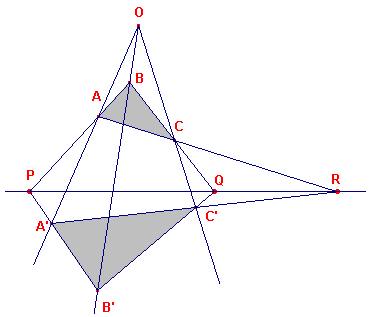
De tekst bij het bovenstaande plaatje (hetzelfde als op die website) moet luiden:
Driehoek BCO met transversaal QC'B' geeft: (BCQ).(COC').(OBB') = 1
Driehoek CAO met transversaal RC'A' geeft: (CAR).(AOA').(OCC') = 1
Driehoek ABO met transversaal PA'B' geeft: (ABP).(BOB').(OAA') = 1
Vermenigvuldiging van die drie uitdrukkingen, links en rechts, geeft (na wat wegstrepen in de deelverhoudingen):
(BCQ)(CAR)(ABP) = 1
waaruit volgt dat de punten Q, R, P collineair zijn.

Namens de webbeheerder van www.pandd.demon.nl vriendelijk dank!
Naar ik begrepen heb, wordt eea. zsm. op die site gecorrigeerd

Zie de pagina Transversalen

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 19 december 2004