WisFaq!

Stelling van Desargues

Het probleem is de hele stelling. Figuur 18a van http://www.pandd.demon.nl/transvers.htm
volgens de stelling van Menelaos zijn de punten collineair als (ABP)(BCQ)(CAR),
maar als ik me niet vergis lees je het zo dat: de lijn AB het snijpunt P met de transversaal opleverd.
maar bij de stelling van desargues zeggen ze dat BC het punt P met de transversaal opleverd.
beetje tegenstrijdig?
hoe zit dit
bij voorbaat bedankt

wilco
16-12-2004

Antwoord

Op de bedoelde pagina is de tekst bij het plaatje onjuist (of eigenlijk: er staat een verkeerd plaatje).



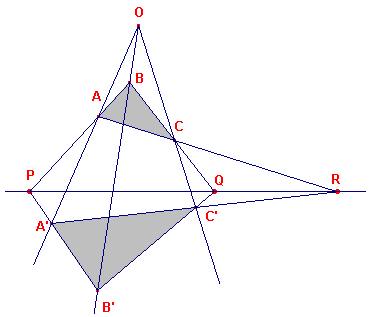
De tekst bij het bovenstaande plaatje (hetzelfde als op die website) moet luiden:
Driehoek BCO met transversaal QC'B' geeft: (BCQ).(COC').(OBB') = 1
Driehoek CAO met transversaal RC'A' geeft: (CAR).(AOA').(OCC') = 1
Driehoek ABO met transversaal PA'B' geeft: (ABP).(BOB').(OAA') = 1
Vermenigvuldiging van die drie uitdrukkingen, links en rechts, geeft (na wat wegstrepen in de deelverhoudingen):
(BCQ)(CAR)(ABP) = 1
waaruit volgt dat de punten Q, R, P collineair zijn.

Namens de webbeheerder van www.pandd.demon.nl vriendelijk dank!
Naar ik begrepen heb, wordt eea. zsm. op die site gecorrigeerd

Zie de pagina Transversalen [http://www.pandd.demon.nl/transvers.htm#74]

dk
19-12-2004