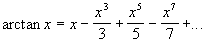WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Benaderen van pi

Dit is een reactie op vraag 16433

euler vond dat
(1/1²)+(1/2²)+(1/3²)+(1/4²)+... = p²/6
Selected Problems from the History of the Infinite Series(onderaan)

dan volgt daaruit toch dat p = Ö6*((1/1²)+(1/2²)+(1/3²)+(1/4²)+...)
hoe komt dat het dan ook gelijk is die andere?
of ben ik ergens fout?
bert
3de graad ASO - maandag 15 november 2004

Antwoord

Iets hoger op dezelfde pagina kun je vinden:

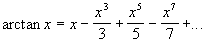
Vul je hier voor x het getal 1 in dan krijg je
arctan(1)=1-1/3+1/5-1/7+1/9-....
p/4=1-1/3+1/5-1/7+1/9-...
p=4*(1-1/3+1/5-1/7+1/9-...)

Je hebt dus nu twee verschillende manieren om p te benaderen.
Waarom zou dit raar zijn? Volgens mij zijn er nog wel meer benaderingsmethoden van p.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 16 november 2004