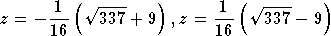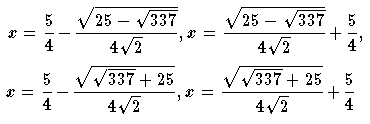De digitale vraagbaak voor het wiskundeonderwijs

home |  vandaag |  gisteren |  bijzonder |  gastenboek |  wie is wie? |  verhalen |  contact

HOME

samengevat

vragen bekijken

een vraag stellen

hulpjes

zoeken

FAQ

links

twitter

boeken

help

inloggen

colofon

Vierdegraadsvergelijking

Is volgende vergelijking op te lossen in als een (dubbele vierkantsvergelijking??) of hoe moet dit aangepakt? Zijn er nu 2 of 4 wortels.
8(2x²-5x+1)²+9(2x²-5x+1)-8=0

Franco
Iets anders - donderdag 30 september 2004

Antwoord

Los eerst 8z²+9z-8=0 op. Dit geeft je twee antwoorden:



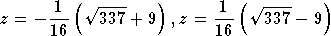
Los vervolgens de volgende twee vergelijkingen op:

2x²-5x+1=-¹/₁₆(Ö337+9)
en
2x²-5x+1=¹/₁₆(Ö337+9)

Dit levert uiteindelijk:



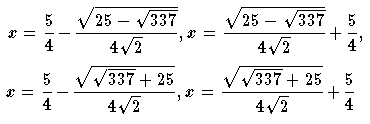
Dit kan je zelf controlen met onderstaand script:

Maar dat stond er blijkbaar niet!
Er stond: 8(2x²-5x+2)²+9(2x²-5x+1)-8=0

Oplossen kan dan met:
8(z+1)²+9z-8=0 oplossen....
Dit geeft 2 oplossingen... alleen z=0 levert dan met
2x²-5x+1=0 de twee reele oplossingen.
Zie eventueel Wat is een complex getal?

Vragen naar aanleiding van dit antwoord? Klik rechts..! zaterdag 2 oktober 2004

home |  vandaag |  bijzonder |  gastenboek |  statistieken |  wie is wie? |  verhalen |  colofon

©2001-2024 WisFaq - versie 3