WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Complexe uitkomst van een machtsverheffing

Hoe bereken ik zonder gebruik te maken van de goniometrische vorm de 3 uitkomsten van Z^5=-32 ?
Thomas
3de graad ASO - donderdag 8 juli 2004

Antwoord

dag Thomas,

Ik weet niet goed wat je bedoelt met de goniometrische vorm, maar er zijn wel 5 uitkomsten in plaats van 3.
De oplossingen liggen in het complexe vlak en vormen een regelmatige vijfhoek.

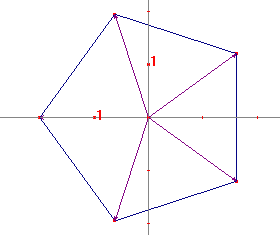
Je kunt ze dan bijvoorbeeld meetkundig bepalen, als je dat leuk vindt.
Ik zou eerlijk gezegd toch gewoon de standaardmethode toepassen:
z⁵ = -32 = 32·e^i·p
dus de modulus van z is de vijfdemachtswortel van 32, dus 2,
en het argument van z is (p + k·2p)/5,
voor k = 0, 1, 2, 3, 4
z_k = 2·e^{i·(p + k·2p)/5}
Voor k=0 vind je zo z₀ = -2
De andere waarden van k corresponderen met de andere hoekpunten van de vijfhoek.
groet,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 8 juli 2004

Re: Complexe uitkomst van een machtsverheffing