|
|
|
\require{AMSmath}



De Poissonverdeling
a.Je hebt 17001 rijtjes van 5 getallen uit de getallen 1,....45. Ze zijn random gekozen.
Bereken de kans dat een rijtje voorkomt dat 4 of meer keer gekozen is, en bereken de kans dat een rijtje 5 of meer keer gekozen is.
Als tip kreeg ik om dit op te vatten als een verjaardagsprobleem, dus met 45nCr5 = 1221 759 mogelijke geboortedagen en 17001 personen.
Het aantal experimenten is 17001nCr4 = n
De succeskans is 1/1221 759 = p
Maar hoe nu verder? Is dit sowieso al goed?
b. Een loterij.
Er zijn 138,5 miljoen rijtjes random ingevuld, er worden 5 witte uit 49 genummerde ballen getrokken en 1 rode uit 42 genummerde ballen.
Wat is de kans dat een gegeven rijtje van 5 Witte en 1 Rode winnend is voor de jackpot.
En wat is de kans op 1 winnaar van de jackpot en wat de kans op meer dan 1 winnaar?
P( R=1 en W=5) = (42nCr1)x(49nCr5) / (91nCr6) +=- 0,12051
Hoe ga je vervolgens verder, bereken je de labda?
Of doe je P(x=1) = poissonpdf(labda,1)
Ik kom echt niet verder dan dit, ik hoop dat jullie mij kunnen helpen.
Bij voorbaat dank
Paulin
Leerling bovenbouw havo-vwo - vrijdag 7 mei 2004
Antwoord
Vraag a. werd al eerder besproken op De poisson verdeling.
b.
Er zijn 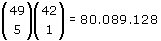 verschillende rijtjes. De kans dat jouw rijtje wordt getrokken is dan 1/80.089.128 verschillende rijtjes. De kans dat jouw rijtje wordt getrokken is dan 1/80.089.128
De kans op 1 winnaar kan je benaderen met de Poisson-verdeling. Het gemiddeld aantal rijtjes goed is:
l=138.500.000/80.089.128 1,729 1,729
We zien: P(X=1) 0,3068 0,3068

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 8 mei 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








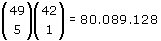 verschillende rijtjes. De kans dat jouw rijtje wordt getrokken is dan 1/80.089.128
verschillende rijtjes. De kans dat jouw rijtje wordt getrokken is dan 1/80.089.128 1,729
1,729
