WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gebroken functie

Hallo,

Ik wil vragen of u wat wilt vertellen over gebroken functies, en dan vooral over de asymtoten en hoe die veranderen als je de functie vermedigvuldigd.

Bijvoorbaat dank
pieter
Leerling bovenbouw havo-vwo - dinsdag 25 november 2003

Antwoord

Hallo Pieter,

Je hebt natuurlijk wel veel verschillende gebroken functies.
Ik ga in het voorbeeld uit van een gebroken lineaire functie.

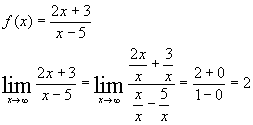
Dit geeft de horizontale asymptoot y = 2
Als je nog niet gewerkt hebt met limieten dan kun je de horizontale asymptoot bepalen met de GRM.
y1 = (2x+3)/(x-5) en kijk dan in de tabel voor een hele grote waarde van x (b.v. 10^12)

De verticale asymptoot kun je vinden door na te gaan wanneer de noemer gelijk wordt aan 0.
In dit voorbeeld is de verticale asymptoot x = 5

Bij vermenigvuldigen t.o.v. de x-as dan blijft de noemer van de beeldfunctie gelijk, dus de verticale asyptoot blijft x = 5. De horizontale asymptoot wordt dan y = 2.factor.

Bij vermenigvuldigen t.o.v. de y – as blijft de horizontale asymptoot y = 2, maar krijgt de verticale asymptoot een andere waarde. Als we bijvoorbeeld de functie vermenivuldigen t.o.v. de y – as met 0,5 dan wordt het beeld g(x) = (4x+3)/(2x-5)
De noemer wordt nu 0 als x = 2,5® verticale asymptoot x = 2,5

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 25 november 2003

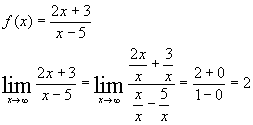
Re: Gebroken functie