Je hebt natuurlijk wel veel verschillende gebroken functies.
Ik ga in het voorbeeld uit van een gebroken lineaire functie.
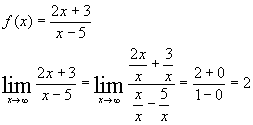
Dit geeft de horizontale asymptoot y = 2
Als je nog niet gewerkt hebt met limieten dan kun je de horizontale asymptoot bepalen met de GRM.
y1 = (2x+3)/(x-5) en kijk dan in de tabel voor een hele grote waarde van x (b.v. 10^12)
De verticale asymptoot kun je vinden door na te gaan wanneer de noemer gelijk wordt aan 0.
In dit voorbeeld is de verticale asymptoot x = 5
Bij vermenigvuldigen t.o.v. de x-as dan blijft de noemer van de beeldfunctie gelijk, dus de verticale asyptoot blijft x = 5. De horizontale asymptoot wordt dan y = 2.factor.
Bij vermenigvuldigen t.o.v. de y – as blijft de horizontale asymptoot y = 2, maar krijgt de verticale asymptoot een andere waarde. Als we bijvoorbeeld de functie vermenivuldigen t.o.v. de y – as met 0,5 dan wordt het beeld g(x) = (4x+3)/(2x-5)
De noemer wordt nu 0 als x = 2,5® verticale asymptoot x = 2,5
wl
25-11-2003