WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Logaritmische en exponentiele vergelijkingen oplossen

Wie kan me helpen? Hoe los je op:
1°) 4^x+7=3.2^1-x+2^2x+1
2°) 2.log₂(x-1)-2.log₄(x²+1)=1-log₄(25)

Alvast bedankt voor de hulp,want ik kom er echt niet uit :-)

Groetjes

Anneke
Anneke
3de graad ASO - zondag 16 november 2003

Antwoord

1°)
Schrijf eerst alles in een vorm waarin 2^x voorkomt. Dus:
2^2x+7=3·2·2^-x+2·(2^x)²
(2^x)²+7=6/2^x+2·(2^x)²

Vervang vervolgens 2^x door y.

y²+7=6/y+2y²
y²+6/y=7
y³+6=7y
y³-7y+6=0
(y-2)(y-1)(y+3)=0
y=2 of y=1 of y=-3

Maar y=2^x, dit levert als (reële) oplossingen:
x=0 of x=1

2°)
Schrijf eerst alles eens als dezelfde logaritme en probeer dan iets te maken als:
log₂(...)=log₂(...)

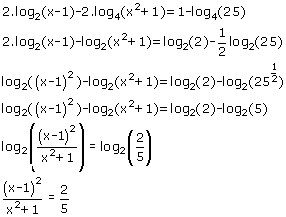
..en dan zal het verder wel lukken toch? Misschien toch nog maar eens de rekenregels machten en logaritmen bestuderen...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 november 2003

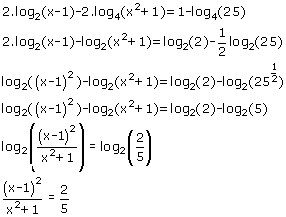
Re: Logaritmische en exponentiele vergelijkingen oplossen