WisFaq!

Logaritmische en exponentiele vergelijkingen oplossen

Wie kan me helpen? Hoe los je op:
1°) 4^x+7=3.2^1-x+2^2x+1
2°) 2.log₂(x-1)-2.log₄(x²+1)=1-log₄(25)

Alvast bedankt voor de hulp,want ik kom er echt niet uit :-)

Groetjes

Anneke

Anneke
16-11-2003

Antwoord

1°)
Schrijf eerst alles in een vorm waarin 2^x voorkomt. Dus:
2^2x+7=3·2·2^-x+2·(2^x)²
(2^x)²+7=6/2^x+2·(2^x)²

Vervang vervolgens 2^x door y.

y²+7=6/y+2y²
y²+6/y=7
y³+6=7y
y³-7y+6=0
(y-2)(y-1)(y+3)=0
y=2 of y=1 of y=-3

Maar y=2^x, dit levert als (reële) oplossingen:
x=0 of x=1

2°)
Schrijf eerst alles eens als dezelfde logaritme en probeer dan iets te maken als:
log₂(...)=log₂(...)



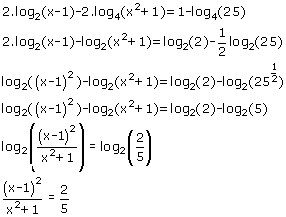
..en dan zal het verder wel lukken toch? Misschien toch nog maar eens de rekenregels machten en logaritmen bestuderen...

WvR
16-11-2003