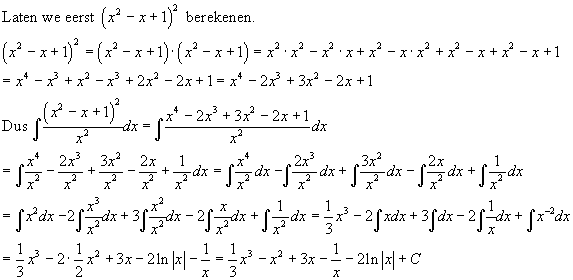|
|
|
\require{AMSmath}



Integreren van een breuk
Hoe integreer ik: dx/x6?
En hoe integreer ik: (x2-x+1)2/x2 dx?
Ik ben net met integraalrekening begonnen omdat ik dat na de vakantie krijg. Alvast bedankt voor de moeite.
Jochem
Student hbo - donderdag 14 augustus 2003
Antwoord
Beste Jochem,
òdx/(x6)
Herschrijf deze integraal als òx-6dx
Gebruik nu de formule òxndx = xn+1/n+1 + C
Dus òx-6dx = -1/5x-5 + C = -1/5·1/x5 + C
ò(x2-x+1)2/x2dx
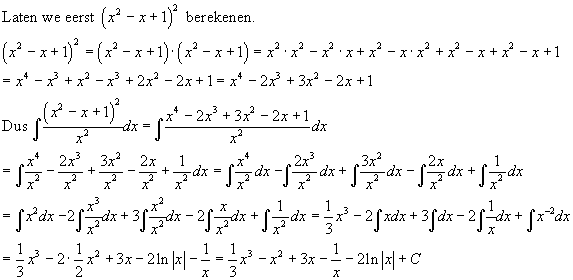
Je moet wel in staat zijn om de standaardfuncties te kunnen integreren. Je moest bijvoorbeeld weten dat
ò1/xdx = ln|x| + C
Indien iets niet duidelijk is, laat 't me weten.
Davy.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 augustus 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|