WisFaq!

Integreren van een breuk

Hoe integreer ik: dx/x⁶?
En hoe integreer ik: (x²-x+1)²/x² dx?

Ik ben net met integraalrekening begonnen omdat ik dat na de vakantie krijg. Alvast bedankt voor de moeite.

Jochem de Bock
14-8-2003

Antwoord

Beste Jochem,

ò^dx/_(x⁶)
Herschrijf deze integraal als òx^-6dx
Gebruik nu de formule òxⁿdx = xⁿ⁺¹/_n+1 + C
Dus òx^-6dx = -¹/₅x^-5 + C = -¹/₅·¹/_x⁵ + C

ò^(x2-x+1)2/_x²dx


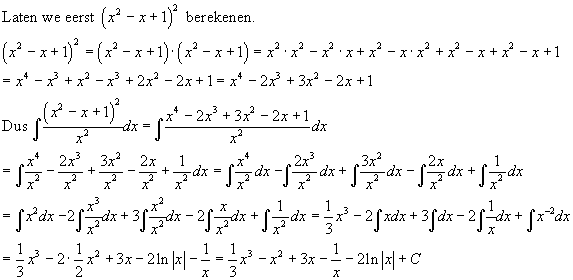
Je moet wel in staat zijn om de standaardfuncties te kunnen integreren. Je moest bijvoorbeeld weten dat
ò¹/_xdx = ln|x| + C

Indien iets niet duidelijk is, laat 't me weten.

Davy.

Davy
14-8-2003