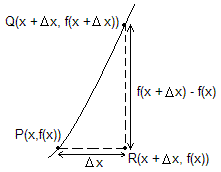|
|
|
\require{AMSmath}
Re: Formule voor de lengte van een curve
Waar vind ik het bewijs hiervoor?
jack h
Student hbo - vrijdag 6 juni 2003
Antwoord
Hoi,
Stel de volgende willekeurige functie voor.
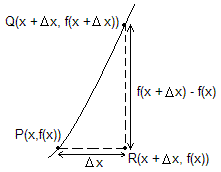
Je wilt de lengte van de grafiek tussen P en Q weten.
Eerst zou je dat kunnen benaderen, door Pythagoras toe te passen. PQ2 = (Dx)2 + (f(x + Dx) - f(x))2 Þ PQ = Ö[(Dx)2 + (f(x + Dx) - f(x))2]
We kunnen (f(x+Dx)-f(x))2 herschrijven als [[f(x + Dx) - f(x) · Dx]/(Dx)]2
Dan staat er iets bekends namelijk [f(x + Dx) - f(x)]/(Dx) en dat is de afgeleide van f.
Dus er staat PQ = Ö[(Dx)2 + (f'(x)·Dx)2]
PQ = Ö [(Dx)2 + (Dx)2·(f'(x))2]
Zetten we (Dx)2 buiten haakjes, krijgen we
PQ = Ö[(Dx)2·(1 + (f'(x))2)]
Indien we (Dx)2 buiten het wortelteken zetten krijgen we PQ = Dx·Ö[1 + (f'(x))2].
Indien we nu het interval [x, x + Dx] in oneindig veel Dx'en verdelen, krijgen we de algemene formule zoals in vorige antwoord gegeven.
Groetjes,
Davy.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 9 juni 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 12116