WisFaq!

Re: Formule voor de lengte van een curve

Waar vind ik het bewijs hiervoor?

jack hielema
6-6-2003

Antwoord

Hoi,

Stel de volgende willekeurige functie voor.

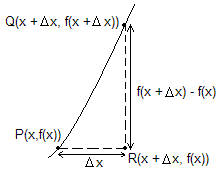
Je wilt de lengte van de grafiek tussen P en Q weten.
Eerst zou je dat kunnen benaderen, door Pythagoras toe te passen. PQ² = (Dx)² + (f(x + Dx) - f(x))² Þ PQ = Ö[(Dx)² + (f(x + Dx) - f(x))²]
We kunnen (f(x+Dx)-f(x))² herschrijven als [[f(x + Dx) - f(x) · Dx]/(Dx)]²
Dan staat er iets bekends namelijk [f(x + Dx) - f(x)]/(Dx) en dat is de afgeleide van f.

Dus er staat PQ = Ö[(Dx)² + (f'(x)·Dx)²]
PQ = Ö [(Dx)² + (Dx)²·(f'(x))²]
Zetten we (Dx)² buiten haakjes, krijgen we
PQ = Ö[(Dx)²·(1 + (f'(x))²)]
Indien we (Dx)² buiten het wortelteken zetten krijgen we PQ = Dx·Ö[1 + (f'(x))²].

Indien we nu het interval [x, x + Dx] in oneindig veel Dx'en verdelen, krijgen we de algemene formule zoals in vorige antwoord gegeven.

Groetjes,

Davy.

Davy
9-6-2003