|
|
|
\require{AMSmath}



Oppervlakte cirkeldeel
Stel, men heeft een cirkel met een straal van 36 mm.
In deze cirkel moet men een cirkelsegment plaatsen met een oppervlak van 22,5 cm². Het nieuw te plaatsen cirkelsegment moet dus ook een straal hebben van 36 mm.
Hoe hoog wordt dan het nieuwe cirkelsegment?
Henk S
Iets anders - dinsdag 3 juni 2003
Antwoord
Beste Henk,
Eerst een aantal belangrijke formules.
Osegment = Osector - Odriehoek = \pi·r2·\alpha°/360° - 1/2r2·sin\alpha.
Hoogte-segment = straal - hoogte driehoek = r(1 - cos1/2\alpha)
in onderstaand algemeen plaatje
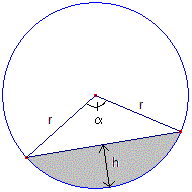
Uit jouw gegevens kun je halen dat r = 3,6 cm, maar niet welke hoek \alpha. Maar je weet wel dat de oppervlakte van het cirkelsegment 221/2 cm2 is, dus kun je de vergelijking
\pi·(3,6)2 · x/360 - 1/2·(3,6)2·sin(x) = 22,5 oplossen.
Dit heb ik Maple laten oplossen, zie onderstaand plaatje.
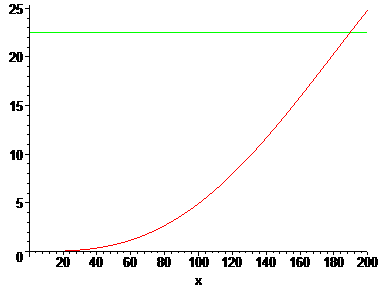
Dit kun je ook zelf via GRM doen. Voer als eerste functie \pi·(3.6)2 · (x/360) - 0.5·(3.6)2·sin((x·\pi/180)) in (zet 'm wel op radialen, dat gedeelte waar de sinus van genomen moet worden wordt automatisch in graden omgezet vanwege de conversie ·\pi/180), en voer als tweede functie 22.5 in. Plot beide functies en bepaal het snijpunt. Het snijpunt is x \approx 189.4935295. Dus voor \alpha = 189.4935295° geldt dat oppervlakte van segment 22,5 cm2 is.
Dan gaan we de formule r(1 - cos1/2\alpha) toepassen.
3,6(1 - cos(94.74676475°)) \approx 3,897906968 (om dit te berekenen moet je rekenmachine uiteraard op graden staan).
Duidelijk?
Groetjes,
Davy.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 3 juni 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|












 Re: Oppervlakte cirkeldeel
Re: Oppervlakte cirkeldeel