WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Aanpak van vergelijkingen

Hallo,

Weet iemand misschien hoe men aan kan tonen bij vergelijkingen dat die functie meer dan 1 oplossing hebben?

Bijvoorbeeld bij deze functies:
A) (x-4).2^x = 2^x
B) (x-4)sinx =sinx

Ik weet wel dat bij deze functies de term discriminant vaak valt wat is dat dan ?

Mijn tweede probleemje is dat ik niet weet hoe ik de regel AB=AC toe kan passen om deze vergelijking op te lossen:
(sinx)²= sinx
Alvast bedankt voor uw antwoord wisfaq

Tim
Leerling bovenbouw havo-vwo - woensdag 21 mei 2003

Antwoord

Hoi Tim,

Oplossing vraag A

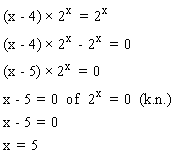
Oplossing vraag B

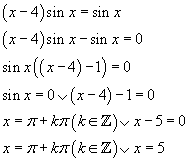
Oplossing vraag C

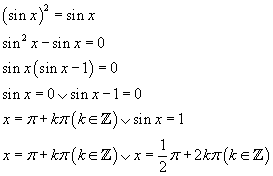
Je algemene vraag was dat je een vergelijking van de vorm AB = AC niet kon oplossen.
Breng het rechterlid naar het linker toe, daardoor verandert het van teken, en wordt de uitkomst 0 (anders waren AB en AC niet aan elkaar gelijk)

AB - AC = 0

Deze twee termen hebben een gemeenschappelijke factor, namelijk A, zet die buiten haakjes (vanwege distributieve eigenschap mag je dat doen)

A(B - C) = 0

Wanneer is een product 0? Indien een van de factoren 0 is, dus

A = 0 of B - C = 0
Nu kun je B - C = 0 nog herschrijven als B = C (indien dit de som gemakkelijker maakt tenminste), het ligt er maar aan wat B en C is... bij sinusoïden (sinus- en cosinusfuncties) is er vaak een verband tussen de snijpunten aangezien die periodiek zijn.

Indien je nog vragen hebt over dit soort problemen hoor ik 't graag van je,

Groetjes,

Davy.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 21 mei 2003

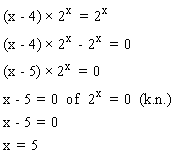
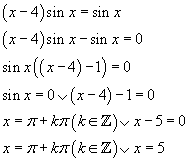
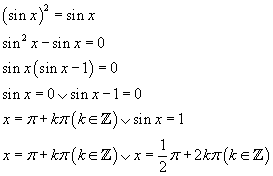
Re: Aanpak van vergelijkingen