WisFaq!

Aanpak van vergelijkingen

Hallo,

Weet iemand misschien hoe men aan kan tonen bij vergelijkingen dat die functie meer dan 1 oplossing hebben?

Bijvoorbeeld bij deze functies:
A) (x-4).2^x = 2^x
B) (x-4)sinx =sinx

Ik weet wel dat bij deze functies de term discriminant vaak valt wat is dat dan ?

Mijn tweede probleemje is dat ik niet weet hoe ik de regel AB=AC toe kan passen om deze vergelijking op te lossen:
(sinx)²= sinx
Alvast bedankt voor uw antwoord wisfaq

Tim
21-5-2003

Antwoord

Hoi Tim,

Oplossing vraag A


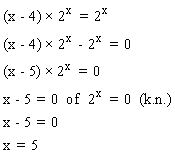
Oplossing vraag B


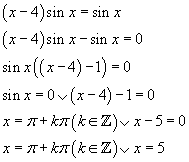
Oplossing vraag C


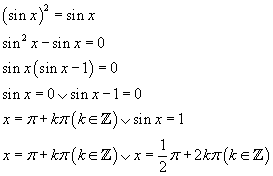
Je algemene vraag was dat je een vergelijking van de vorm AB = AC niet kon oplossen.
Breng het rechterlid naar het linker toe, daardoor verandert het van teken, en wordt de uitkomst 0 (anders waren AB en AC niet aan elkaar gelijk)

AB - AC = 0

Deze twee termen hebben een gemeenschappelijke factor, namelijk A, zet die buiten haakjes (vanwege distributieve eigenschap mag je dat doen)

A(B - C) = 0

Wanneer is een product 0? Indien een van de factoren 0 is, dus

A = 0 of B - C = 0
Nu kun je B - C = 0 nog herschrijven als B = C (indien dit de som gemakkelijker maakt tenminste), het ligt er maar aan wat B en C is... bij sinusoïden (sinus- en cosinusfuncties) is er vaak een verband tussen de snijpunten aangezien die periodiek zijn.

Indien je nog vragen hebt over dit soort problemen hoor ik 't graag van je,

Groetjes,

Davy.

Davy
21-5-2003