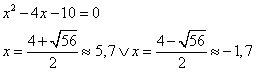WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Derdegraadsvergelijking

Dit is een reactie op vraag 1620

hay!Wij moeten ook een po maken over derdegraadsvergelijkingen. We hebben dit voorbeeld bekeken maar snappen niet waar die `s` vandaan komt en waarom je de formule door `x-s´ moet delen. Kunnen jullie dit misschien op een makkelijkere manier uitleggen??? Alvast dankjewel....Sjmer en Vannies
nadine
Leerling bovenbouw havo-vwo - zaterdag 26 april 2003

Antwoord

Als je alle oplossingen van een derdegraadsvergelijking wilt vinden, moet je je realiseren dat er altijd minstens één is. Probeer maar eens wat verschillende grafieken te plotten, door in y=x³+ax²+bx+c verschillende waarden voor a, b en c in te vullen.
Stel je nu voor dat je een oplossing, x=s, van de vergelijking kent (die zie je bijvoorbeeld gemakkelijk zitten, omdat je dat bijvoorbeeld in een tabel ziet). Door nu te delen door (x-s) houd je een tweedegraadsvergelijking over, en die kun je simpel met de abc-formule aanpakken.

Een voorbeeld: x³-5x²-6x+10=0.
Je ziet makkelijk dat x=1 een oplossing is.
Delen door x-1 geeft: x²-4x-10=0
(kijk bij het antwoord van je oorspronkelijke vraag hoe dat moet)
En nu de abc-formule:

En nu heb je alle oplossingen gevonden. Deze methode 'doet het' dus alleen als je één oplossing kunt vinden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 26 april 2003