\require{AMSmath}

Formule eindkapitaal bij vaste inleg

Hoe luidt de formule om het eindkapitaal uit te kunnen rekenen bij een maandelijkse vaste inleg tegen een vast percentage voor een bepaalde duur?

Bijvoorbeeld: fl. 300,= gedurende 20 jaar tegen 7%?

Jan Wi
Iets anders - dinsdag 21 augustus 2001

Antwoord

Een 'kort' antwoord zou kunnen luiden:

met:

m	de maandelijkse inleg
p	het rentepercentage
l	de looptijd in jaren

Erg bevredigend is zo'n antwoord niet. Vandaar wat toelichting.Eerst een paar vooronderstellingen om het probleem beter hanteerbaar te maken:

1. We doen net alsof alle maanden even lang zijn
2. Elke maand wordt de rente bijgeschreven
3. Alleen geld dat een maand of langer op de rekening staat levert rente op

We moeten allereerst de maandelijkse rente berekenen.
De groeifactor per jaar bij een rentepercentage p is 1+ 0,01p ; Bij een rentepercentage van 7 dus 1,07.
De groeifactor per maand is (1+0,01p)^(1/12). Bij 7 % rente 1,07^(1/12) = 1,005654 (ongeveer)De maandelijkse rente bedraagt dus ca 0,5654 %

Hiermee kunnen we een recursievergelijking opstellen:

B(t) = 1,005654 × B(t-1) + 300 (t>1) en B(0) = 300

Hier is B(t) het bedrag na t maanden (gerekend vanaf de eerste inleg).In feite zegt de recursievergelijking dat het bedrag op een bepaald moment 1,005654 maal het bedrag van een maand geleden is (vanweg de rentebijschrijving) plus 300 (de inleg)Het invoeren van deze vergelijking in een grafische rekenmachine (of een spreadheet zoals Excel) geeft snel de situatie over 20 jaar.

Het kan echter ook met een directe formule.Deze formule bestaat uit twee delen die bij elkaar opgeteld dienen te worden (en een kleine correctie)

1. De evenwichtswaarde
   Wanneer je een schuld begint kan het zo zijn dat de maandelijkse inleg precies voldoende is om de rente te betalen. Dit gebeurt bij een aflossingvrije hypotheek. Als we dit bedrag E noemen moet gelden:
   0,005654 × E + 300 = 0 Dus E = - 300 / 0,005654 = -53058,42 (gld)]In het algemeen geldt: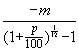

   of te wel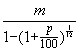

2. De bedragen op de bank vormen - als we steeds een maand verder kijken - een combimnatie van een rekenkundige rij (steeds de zelfde inleg erbij) en een meetkundige rij (steeds vermenigvuldigen met het zelfde getal ivm de rentebijschrijving). Dit maakt het lastig om snel te berekenen watde situatie over bijv 10 jaar is. Echter wanneer we kijken naar het verschil met de evenwichtswaarde krijgen we een 'eenvoudige' meetkundige rij, waar we snel mee kunnen rekenen. De groeifactor van dit verschil is ('gewoon') de groeifactor die hoort bij het rentepercentage - in ons voorbeeld 1,07 (per jaar).Het verschil met E bedraagt in het begin 300 - E = 53 358,42Om het verschil na 20 jaar te berekenen hoeven we dit alleen te vermenigvuldigen met 1,07²⁰Dit levert een bedrag op van ruim 2 ton : 206 480,23 (gld)De algemene formule luidt:

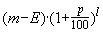
   Hierbij is E de evenwichtswaarde van deel 1 en l de looptijd (in jaren)

3. Na 20 jaar (240 maanden) wordt er geen 300 gulden meer ingelegd, terwijl we in de berekening doen alsof dat wel zo is . We moeten dus nog 300 van het totaal aftrekken

Wanneer we bovenstaande combineren komen we uit op een eindbedrag van fl 153.121,82. Dit klopt met de on-line berekenig op de website van de NVA (makelaars) "Indicatie eindbedrag: 153.122 gulden."

gk
maandag 27 augustus 2001

Re: Formule eindkapitaal bij vaste inleg

Re: Formule eindkapitaal bij vaste inleg

Re: Formule eindkapitaal bij vaste inleg

©2001-2024 WisFaq