|
|
|
\require{AMSmath}



Re: Oppervlakte bolwoning
Hallo,
Bedankt voor uw uitleg. Ik heb dit verder gbruikt om de Inhoud te berekenen.
waarbij gebruikt gemaakt moet worden van de formule voor de inhoud van een bolsegment met hoogte h van een bol met straal r.
De inhoud van zo'n bolsegment is: 1/3$\pi$h2(3R-h).
De inhoud=
4/3$\pi$·43-1/3$\pi$(4-√2-32)2(3·4-(4-√42-32))+$\pi$·32·3 337,8 m3 337,8 m3
Inhoud Woning=inhoud bol-inhoudbolsegment+inhoud cilinder
Waarmee ik voordat ik begin mee in de war raak is het volgende en tevens mijn vraag:
Inhoud bolsegment= 1/6$\pi$h(3r2+h2)
Moet ik nu het bolsegment zien als een Kegel, zoals in de opgave omschreven is met inhoud=1/3$\pi$h2(3R-h).?
Wat is het verschil tussen beide formules en waarom?
En zo ook bij het vorige waar de Oppervlakte gevraagd wordt, volgens de opgave met
oppervlakte bolsegment=2$\pi$rh
Waarom is hier:
oppervlakte bolsegment=oppervlakte cilinder
En niet oppervlakte bolkap=$\pi$·(r2+h2)
Waar ik over struikel met de formules die in de opgave worden gegeven voor de oppervlakte en de inhoud, is dat nergens wordt gesproken over cirkelsectoren, de hoek en hoogte waarop de cilinder de bol raakt.
Of is dit gewoonweg niet van toepassing?
Bij voorbaat mijn dank.
Groet Kees
Kees
Leerling bovenbouw havo-vwo - vrijdag 20 januari 2017
Antwoord
Hallo Kees,
Een bolsegment is geen kegel, de formule die in de opgave staat is ook niet de formule voor de inhoud van een kegel.
Voor de inhoud van een bolkap bestaan twee formules:
Inhoud = 1/6$\pi$h(3r2+h2) (formule 1)
Inhoud = 1/3$\pi$h2(3R-h) (formule 2)
Let erop dat r in formule 1 niet hetzelfde is als R in formule 2! R is de straal van de bol, r is de straal van de bolkap (dus de straal van het 'grondvlak' van de bolkap), zie onderstaande figuur:
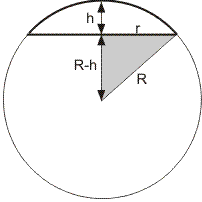
R = straal bol
r = straal bolkap
h = hoogte bolkap
Toch zijn deze formules in feite hetzelfde. Immers, volgens Pythagoras geldt:
r2 = R2-(R-h)2
Haakjes wegwerken levert:
r2 = 2Rh-h2
Vul dit in formule (1) in:
Inhoud = 1/6$\pi$h(3(2Rh-h2)+h2)
Inhoud = 1/6$\pi$h(6Rh-3h2+h2)
Inhoud = 1/6$\pi$h(6Rh-2h2)
Inhoud = 1/3$\pi$h2(3R-h)
Nu heb je formule (2) gekregen.
Dan jouw vraag 'Waarom is hier: oppervlakte bolsegment=oppervlakte cilinder." Hiermee maak je een belangrijke vergissing. Voor de oppervlakte van een cilindermantel geldt inderdaad de formule:
oppcilinder = 2$\pi$rh, waarbij r de straal is van het cirkelvormige grondvlak van de cilinder.
Voor de oppervlakte van een bolkap geldt de formule:
oppbolkap=2$\pi$Rh, hierin is R de straal van de bol, niet de straal van de bolkap. Je moet deze twee stralen niet door elkaar halen!
Tot slot jouw laatste punt: je struikelt over formules voor oppervlakte en inhoud, er is niets gegeven over de hoek en hoogte waarop de cilinder de bol raakt.
Twee dingen lijken me belangrijk: wanneer de straal van de bol gegeven is (R=8) en de straal van de cilinder (r=6), dan kan je zelf berekenen hoe hoog de bolkap is die in de cilinder 'wegzakt', zie mijn antwoord op jouw vorige vraag. Dit is onderdeel van de opdracht. Hiervoor moet je een nette schets maken (=eerste belangrijke punt).
Vervolgens moet je de formules netjes en zorgvuldig uitwerken (=tweede belangrijke punt). Zet duidelijke letters in je figuur (h, R) en als je te maken hebt met twee verschillende stralen (hier: van de bol en van de cilinder), gebruik dan duidelijk verschillende symbolen, zodat je niet de bolstraal in de formule voor een cilinder invult of andersom. Neem kleine stappen (bv bij wegwerken van haakjes), hiermee voorkom je vergissingen.
Hopelijk helpt dit.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 20 januari 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 83702
Dit is een reactie op vraag 83702  337,8 m3
337,8 m3

