WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte bolwoning

Hallo,
Mijn vraag gaat over een gedeelte van de formule van een bolwoning:

In 's-Hertogenbosch staan vijftig bolwoningen die in 1984 zijn gebouwd, deze zijn ontworpen door de beeldhouwer, ontwerper en architect Dries Kreijkamp.

Welke oppervlakte hebben deze bolwoningen als de diameter van de bol zelf 8 meter en die van de cilinder 6 meter is, terwijl de hoogte van de cilinder 3 meter is?
Maak hierbij gebruik van de formule voor de oppervlakte van een bolsegment met hoogte h van een bol met straal r.
De oppervlakte van zo'n bolsegment is 2$\pi$rh.

Oplossing:
Oppervlakte van een cilinder= 2$\pi$r·h
Voor de bol geldt h=2r
Oppervlakte bol 2$\pi$r·2r= 4$\pi$r²
Oppervlakte bolkap= $\pi$·(r²+h²)

Invullen:
Oppervlakte= 4$\pi$·4²-($\pi$·(3²+4²))+2$\pi$·3·3=
Oppervlakte= opp.bol-bolkap+opp.cilinder.

Ik kom dus niet op het gewenste antwoord uit van 223,6m².
Dat als oplossing wordt gegeven met de formule:
Opp= 4$\pi$·4²-2·$\pi$·4·(4-√4²-3²)+2$\pi$·3·3
=223,6m²

Mijn vraag gaat over het gedeelte
-2·$\pi$·4·(4-√4²-3²)

Waar komt de 2 vandaan is dit nu het verschil tussen beide diameter 8-6. Of van de tekst "De oppervlakte van zo'n bolsegment is 2$\pi$rh".??
Mijn insziens komt het van de tekst.

Maar daar komt mijn tweede vraag dan uit voort
-2·$\pi$·4·(4-√4²-3²)
De oppervlakte van zo'n bolsegment is 2$\pi$rh
2$\pi$
r=4
h=4-√4²-3²

Waarom de eerste 4, ik weet dat het de straal van de bol is, maar waarom niet de straal van de cilinder, deze opp. gaat er immers vanaf.

Waarom het minteken onder de wortel, er staat Pythagoras waaruit je kunt afleiden dat je de schuine/bolvormige zijde al hebt, ik begrijp niet waar ze deze schuine zijde vandaan hebben, ik kom niet verder dan √4²+3².

Ik begrijp gewoon niet zo goed waarom de formule van een bolsegment 2$\pi$rh omgeschreven is in de formule
-2·$\pi$·4·(4-√4²-3²).

Kunt u mij hierbij helpen, waarschijnlijk kijk ik er helemaal verkeerd naar.

Groet Kees
Kees
Leerling bovenbouw havo-vwo - donderdag 12 januari 2017

Antwoord

Hallo Kees,

Zie deze doorsnede van de bolwoning:

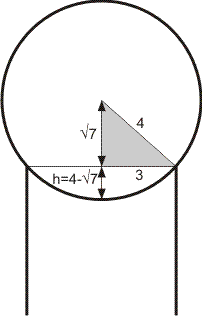
In het grijze driehoekje zie je met behulp van Pythagoras dat de afstand tussen bovenrand cilinder en middelpunt bol gelijk is aan √(4²-3²) = √7. Dan blijft over voor de hoogte h van het bolsegment:

h = r-√7 = 4-√7

De oppervlakte van het bolsegment is dan:

Opp_bolsegment = 2$\pi$rh = 8$\pi$(4-√7)

Invullen levert:

Opp_woning = opp_cilinder + opp_bol - opp_bolsegment

Opp_woning = 18$\pi$ + 64$\pi$ - 8$\pi$(4-√7) = 223,6 m².

Overigens kan je de oppervlakte van het deel van de bol boven de cilinder ook als één segment beschouwen, met hoogte r+√7 = 4+√7. Dan geldt in één keer:

Opp_woning = opp_cilinder + opp_bolsegment

Opp_woning = 18$\pi$ + 8$\pi$(4+√7) = 223,6 m².

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 januari 2017

Re: Oppervlakte bolwoning