|
|
|
\require{AMSmath}



Tangensregel
Ik ken de tangensregel:
(a-b)/(a+b)=(tan(1/2(a-b)))/(tan(1/2(a+b)))
Ik heb ook geprobeerd deze te bewijzen, wat me niet is gelukt. Hoe doe ik dit dan wel?
Marco
Leerling bovenbouw havo-vwo - maandag 17 maart 2008
Antwoord
Hallo
Ik geef eerst een variant op de sinusregel.
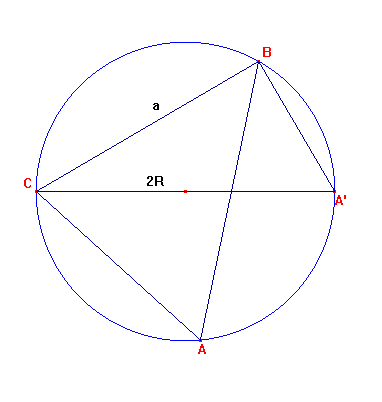
In onderstaande driehoek A'BC, die rechthoekig is in B, geldt:
sin A' = a/2R met R is de straal van de omgeschreven cirkel.
Vermits de hoeken A en A' gelijk zijn (het zijn omtrekshoeken op dezelfde boog BC) geldt ook in de driehoek ABC dat sin A = a/2R
Dit is dus een variant op de sinusregel in een willekeurige driehoek.
Vervang nu in a-b/a+b:
a = 2R.sin A en
b = 2R.sin B
Deel 2R weg in teller en noemer.
Volgens de formule van Simpson geldt
sin A + sin B = 2.sinA+B/2.cosA-B/2
Doe dit ook voor sin A - sin B in de teller.
En dan ben je er wel ...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 17 maart 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










