WisFaq!

Tangensregel

Ik ken de tangensregel:
(a-b)/(a+b)=(tan(¹/₂(a-b)))/(tan(¹/₂(a+b)))
Ik heb ook geprobeerd deze te bewijzen, wat me niet is gelukt. Hoe doe ik dit dan wel?

Marco
17-3-2008

Antwoord

Hallo

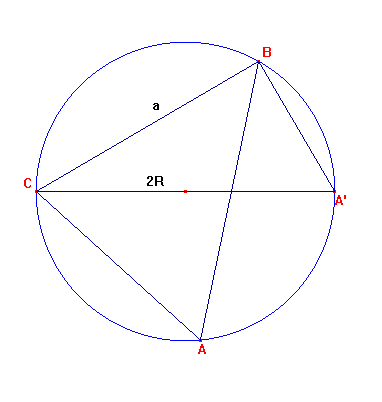
Ik geef eerst een variant op de sinusregel.
In onderstaande driehoek A'BC, die rechthoekig is in B, geldt:
sin A' = ^a/_2R met R is de straal van de omgeschreven cirkel.
Vermits de hoeken A en A' gelijk zijn (het zijn omtrekshoeken op dezelfde boog BC) geldt ook in de driehoek ABC dat sin A = ^a/_2R

Dit is dus een variant op de sinusregel in een willekeurige driehoek.

Vervang nu in ^a-b/_a+b:
a = 2R.sin A en
b = 2R.sin B

Deel 2R weg in teller en noemer.
Volgens de formule van Simpson geldt
sin A + sin B = 2.sin^A+B/₂.cos^A-B/₂
Doe dit ook voor sin A - sin B in de teller.
En dan ben je er wel ...

LL
17-3-2008