|
|
|
\require{AMSmath}
Re: Doorsnede met een hulpconstructie
Ik zie niet hoe je aan dat punt kan geraken?
Dit snap ik dus niet: "ik ga een punt P construeren op KJ dat ligt in het vlak ADHE. Als ik dat heb kan ik IP tekenen"
Maar ik denk dat ik wel zie dat als je P hebt en blijkbaar P met I mag verbinden dat de rest gevonden kan worden door de stelling van de evenwijdigen niet? Denk ik toch.:)
Kunt nog eens even uitleggen hoe het juist zit met dat punt P aub? Want daar loop ik dus al vast natuurlijk.
Bedankt voor uw antwoord.
Vicky
3de graad ASO - zondag 17 december 2006
Antwoord
De lijn KJ ligt in het vlak CGJ. Als je dat vlak snijdt met het vlak ADHE dan krijg je een (verticale) snijlijn. Als deze snijlijn snijdt met KJ dan heb je punt P. Zou dat lukken?
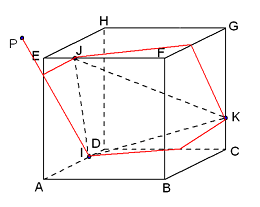
En ja... als je IP eenmaal hebt volgt de rest vrij makkelijk met de stelling over de evenwijdige snijlijnen bij evenwijdige vlakken. In de zeshoek zijn de zijden steeds twee aan twee evenwijdig.
Lastig he? Maar de 'truuk' met zo'n extra punt, dat is toch wel handig vind ik zelf...
Probeer 't maar 's!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 17 december 2006
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 48098