WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

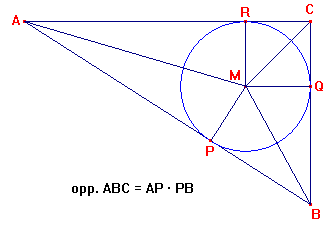
Bewijs voor de stelling van Wolf

Ik heb de opdracht gekregen om de stelling van Wolf uit te zoeken.
De gegevens zijn: rechthoekige driehoek ABC met een ingeschreven cirkel die de driehoek raakt op P, Q en R.
Te bewijzen: opp. ABC= AP·PB

Ik kom hier echter niet uit...
opp ABC= ½·AC·CB
opp ABC=½·AC·(CQ+QB)
QB=PB (bissectrice)
opp ABC= ½·AC·(CQ+PB)
opp ABC= ½·(AR+RC)·(CQ+PB)
AB=AP (bissectrice)
opp ABC= ½·(AP+RC)·(CQ+PB)
CR=CQ
opp ABC= ½·(AP+CQ)·(CQ+PB)
Jerney
Leerling bovenbouw havo-vwo - zaterdag 24 augustus 2002

Antwoord

Je bent een aardig eind op weg. Bedenk dat je ook nog de stelling van Pythagoras kunt gebruiken:
AB² = AC² + CB²
ofwel
(AP + PB)² = (AR + RC)² + (CQ + QB)²
Werk de haakjes weg en gebruik de bisectrice-eigenschap om factoren tegen elkaar te laten wegvallen en probeer de overige stukjes in het plaatje hieronder in te passen.

Applet werkt niet meer.
Download het bestand.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 augustus 2002