WisFaq!

Bewijs voor de stelling van Wolf

Ik heb de opdracht gekregen om de stelling van Wolf uit te zoeken.
De gegevens zijn: rechthoekige driehoek ABC met een ingeschreven cirkel die de driehoek raakt op P, Q en R.
Te bewijzen: opp. ABC= AP·PB

Ik kom hier echter niet uit...

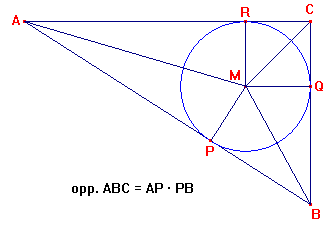
opp ABC= ½·AC·CB
opp ABC=½·AC·(CQ+QB)
QB=PB (bissectrice)
opp ABC= ½·AC·(CQ+PB)
opp ABC= ½·(AR+RC)·(CQ+PB)
AB=AP (bissectrice)
opp ABC= ½·(AP+RC)·(CQ+PB)
CR=CQ
opp ABC= ½·(AP+CQ)·(CQ+PB)

Jerney
24-8-2002

Antwoord

Je bent een aardig eind op weg. Bedenk dat je ook nog de stelling van Pythagoras kunt gebruiken:
AB² = AC² + CB²
ofwel
(AP + PB)² = (AR + RC)² + (CQ + QB)²
Werk de haakjes weg en gebruik de bisectrice-eigenschap om factoren tegen elkaar te laten wegvallen en probeer de overige stukjes in het plaatje hieronder in te passen.

Applet werkt niet meer.
Download het bestand.

wh
26-8-2002