WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Machtreeks sinus en nauwkeurigheid

Deze vraag moeten wij beantwoorden: onderzoek voor verschillende waarden van x na hoeveel termen je de reeks voor sin x mag afkappen om sin x op 1 decimaal nauwkeurig te benaderen. formuleer een vuistregel waarmee je bij een gekozen nauwkeurigheid voor verschillende waarden van x het aantal termen kunt vinden. We hopen dat iemand hier het antwoord op weet, want wij zijn radeloos. Groeten van Lisa en Tim uit Deventer
Lisa e
Leerling bovenbouw havo-vwo - dinsdag 23 april 2002

Antwoord

Eerst maar eens de machtreeks voor de sinus:

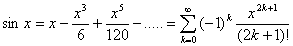
Vervolgens zou je kunnen kijken voor verschillende waarde van x hoeveel termen je nodig hebt voor een benadering die nauwkeurig is op 1 decimaal.

Voorbeeld
Neem x=1 (radialen!)
sin(1)=0,841
Met de machtreeks: sin(1)=1-1³/6=0,833
Deze benadering is al goed... dus 2 termen.

sin(2)=0,909
Met de machtreeks: 2-2³/6=0,667 nee, niet erg goed...
Dan 2-2³/6+2⁵/120=0,933
Dus hier heb je 3 termen nodig...

sin(3)=0,141
3-3³/6=-1,5
3-3³/6+3⁵/120=0,12
Dus ook 3 termen nodig...

Enzovoort...

Voorlopige conclusie
Met 3 termen kan je een benadering voor de sinus vinden op 1 decimaal nauwkeurig. (Verder onderzoek zeer gewenst!)
Voor een vuistregel moet je hetzelfde doen voor 2 decimalen nauwkeurig... 3 decimalen nauwkeurig... en misschien dat je dan al een idee hebt voor de vuistregel (zoiets als 3 termen per decimaal? gokje!). Zelf zou ik toch proberen hier de computer in te zetten...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 april 2002

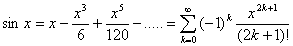
Re: Machtreeks sinus en nauwkeurigheid