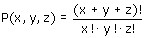|
|
|
\require{AMSmath}



Piramide van Pascal
Ik moet weten hoe de drie dimensionale driehoek van Pascal net zo bruikbaar is in de algebra als het Binomium van Newton. Please ook een formule..
anonie
Leerling bovenbouw havo-vwo - donderdag 18 april 2002
Antwoord
Zoals je op Piramide van Pascal kan lezen kan je in een 3d-rooster de volgende functie declareren:
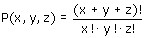
Hiermee kan je uitrekenen op hoeveel manieren je van (0,0,0) naar (x,y,z) kan komen. De vraag is kan je daar nou iets mee?
Voorbeeld
Ik wil (a+b+c)10 berekenen, maar eigenlijk liever niet, want ik ben alleen maar geinterresseerd in de term a5b2c3. Ik weet dat deze term ergens in de uitwerking van (a+b+c)10 voorkomt, maar welke coŽfficiŽnt staat er voor deze term?
Het antwoord is P(5,2,3)=2520, dus ergens in de uitwerking van (a+b+c)10 staat 2520∑a5b2c3.
Voorbeeld
Ik wil graag de coŽfficiŽnt weten van de term a2b3c6 van (2a+3b+4c)11
P(2,3,6)=4620
De term bestaat uit 4620∑(2a)2(3b)3(4c)6=4620∑442368∑a2b3c6 dus de gezochte coŽfficiŽnt is 4620∑442368=2043740160
Of het veel gebruikt wordt weet ik niet, maar het is in ieder geval handiger dan (2a+3b+4c)11 helemaal uitschrijven...
Voorlopige conclusie: Bruikbaar is het zeker, maar of het veel gebruikt wordt....?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 22 april 2002
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|