WisFaq!

Piramide van Pascal

Ik moet weten hoe de drie dimensionale driehoek van Pascal net zo bruikbaar is in de algebra als het Binomium van Newton. Please ook een formule..

anoniem
18-4-2002

Antwoord

Zoals je op Piramide van Pascal kan lezen kan je in een 3d-rooster de volgende functie declareren:



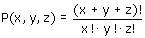
Hiermee kan je uitrekenen op hoeveel manieren je van (0,0,0) naar (x,y,z) kan komen. De vraag is kan je daar nou iets mee?

Voorbeeld
Ik wil (a+b+c)¹⁰ berekenen, maar eigenlijk liever niet, want ik ben alleen maar geinterresseerd in de term a⁵b²c³. Ik weet dat deze term ergens in de uitwerking van (a+b+c)¹⁰ voorkomt, maar welke coëfficiënt staat er voor deze term?
Het antwoord is P(5,2,3)=2520, dus ergens in de uitwerking van (a+b+c)¹⁰ staat 2520·a⁵b²c³.

Voorbeeld
Ik wil graag de coëfficiënt weten van de term a²b³c⁶ van (2a+3b+4c)¹¹
P(2,3,6)=4620
De term bestaat uit 4620·(2a)²(3b)³(4c)⁶=4620·442368·a²b³c⁶ dus de gezochte coëfficiënt is 4620·442368=2043740160
Of het veel gebruikt wordt weet ik niet, maar het is in ieder geval handiger dan (2a+3b+4c)¹¹ helemaal uitschrijven...

Voorlopige conclusie: Bruikbaar is het zeker, maar of het veel gebruikt wordt....?

WvR
22-4-2002