Voorbeeld 1
'Ik wil de maximale oppervlakte van een rechthoekig veld dat met een schutting van 80 m omheind kan worden, als gebruik wordt gemaakt van een muur die aan de overige zijde staat. Deze muur mag zo lang als nodig.'
Uitwerking
 Neem voor lengte van de zijde aan de muurkant 'x'. De zijde evenwijdig aan de muur is dan 80-2x. Stel een formule op voor de oppervlakte van het veld, dus:
Neem voor lengte van de zijde aan de muurkant 'x'. De zijde evenwijdig aan de muur is dan 80-2x. Stel een formule op voor de oppervlakte van het veld, dus:
O(x)=x·(80-2x)=80x-2x2
Bepaal de afgeleide van O(x):
O'(x)=80-4x
Bereken x zodat O'(x)=0. Dit geeft x=20. Controleer met een tekenverloop of met je GR dat x=20 inderdaad een maximum van O(x) oplevert.
Antwoord
Voor x=20 heb je de maximale oppervlakte.
Voorbeeld 2
Gegeven is de functie f(x)= -0,5x2 + 3x.
Van een rechthoek ABCD liggen de punten A en B op de x-as en de punten C en D op de grafiek van f.
Verder is 0$\leq x_A \leq$3.
-
Neem $x_A=p$ en druk de omtrek van ABCD uit in $p$.
-
Bereken de maximale omtrek die rechthoek ABCD kan hebben.
-
Druk de oppervlakte van ABCD uit in $p$.
-
Voor welke $p$ is O(ABCD) maximaal? Bereken in twee decimalen nauwkeurig de maximale oppervlakte die ABCD kan hebben.
Uitwerking
Maak eerst een tekening:
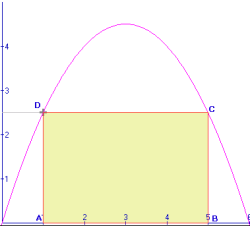
Er geldt A(p,0). Druk AB en BC uit in p. Je krijgt dan:
-
AB=CD=6-2p
-
BC=DA=-0,5p2 + 3p
Je kunt dan de vragen beantwoorden.
-
Omtrek(ABCD)=-p2+2p+12
-
Bereken de afgeleide. O'(x)=-2p+2
Stel de afgeleide nul en los op!
-2p+2=0
p=1
Plot de grafiek... is het een maximum? Zo ja, dan is de omtrek maximaal -12+2·1+12=-1+2+12=13
-
Opp.(ABCD)=p3-9p2+18p
-
Bereken de afgeleide: O'(x)=3p2-18p+18.
Stel de afgeleide nul en los op!
3p2-18p+18=0
p2-6p+6=0
Enz...
Plot de grafiek. Waar is er sprake van een maximum? De maximale oppervlakte is...
Antwoorden
-
Omtrek(ABCD)=-p2+2p+12
-
Maximale omtrek is 13
-
Opp.(ABCD)=p3-9p2+18p
-
Maximale oppervlakte is $6\sqrt{3}$
Voorbeeld 3
Een puntgevel heeft een basis van 10 m en hoogte van 4 m. In de gevel moet een zo groot mogelijk rechthoekig venster komen. Wat zijn de afmetingen van dat venster?
Uitwerking
Maak een tekening en kies (handig) een variabele. In dit geval heb ik voor de lengte van de rechthoek 2x gekozen. Probeer daarna de hoogte uit te drukken in x. Stel een formule op voor de oppervlakte en probeer de oppervlakte te maximaliseren.
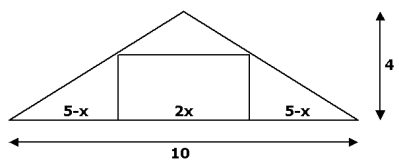
$
\eqalign{
& \frac{5}
{4} = \frac{{5 - x}}
{h} \Rightarrow 5h = 20 - 4x \Rightarrow h = 4 - \frac{4}
{5}x \cr
& O(x) = 2x \cdot \left( {4 - \frac{4}
{5}x} \right) = 8x - \frac{8}
{5}x^{2} \cr
& O'(x) = 8 - \frac{{16}}
{5}x \cr
& O'(x) = 0:8 - \frac{{16}}
{5}x = 0 \cr
& \frac{{16}}
{5}x = 8 \cr
& 16x = 40 \cr
& x = 2\frac{1}
{2} \cr}
$
Antwoord
De rechthoek is 5 bij 2.
Voorbeeld 4
Drie zijden van een gelijkbenig trapezium zijn 10 cm lang. hoe lang moet de vierde zijde zijn om een maximale oppervlakte van het trapezium te hebben?
Uitwerking
Eerst maar weer eens een tekening:
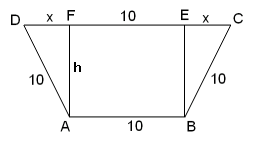
Druk h uit in x. Stel dan een formule op voor de oppervlakte van het trapezium en probeer deze functie te maximaliseren.
$
\eqalign{
& h = \sqrt {100 - x^{2} } \cr
& O(x) = \frac{{10 + 10 + 2x}}
{2} \cdot \sqrt {100 - x^{2} } = \left( {10 + x} \right) \cdot \sqrt {100 - x^{2} } \cr
& O'(x) = \sqrt {100 - x^{2} } + \left( {10 + x} \right) \cdot - \frac{x}
{{\sqrt {100 - x^{2} } }} \cr
& O'(x) = \sqrt {100 - x^{2} } - \frac{{10x + x^{2} }}
{{\sqrt {100 - x^{2} } }} \cr
& O'(x) = \frac{{100 - x^{2} - 10x - x^{2} }}
{{\sqrt {100 - x^{2} } }} = \frac{{100 - 10x - 2x^{2} }}
{{\sqrt {100 - x^{2} } }} = 0 \cr
& 100 - 10x - 2x^{2} = 0 \cr
& 50 - 5x - x^{2} = 0 \cr
& x^{2} + 5x - 50 = 0 \cr
& (x - 5)(x + 10) = 0 \cr
& x = 5 \vee x = - 10 \cr
& Alleen\,\,x = 5\,\,voldoet. \cr}
$
Antwoord
De vierde zijde moet 20 zijn.
Meer voorbeelden

