\require{AMSmath}

Re: Voorschrift vinden

Dit is een reactie op vraag 98420

Bedankt, het lijkt zo simpel, maar is er een methode daarvoor? Bv elke rechte apart proberen te vinden, dan een stelsel van maken?
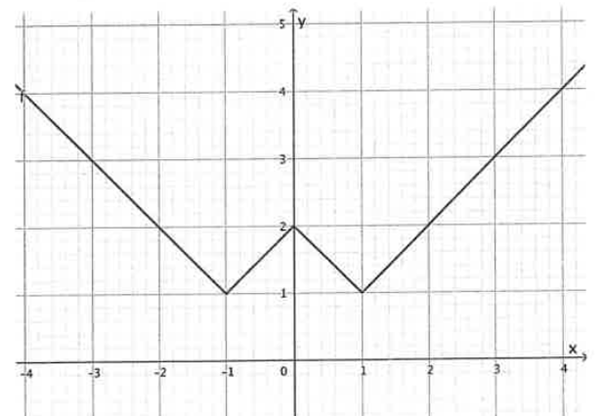
Bv: hoe pak je deze nieuwe grafiek aan?

3de graad ASO - zaterdag 28 december 2024

Antwoord

Je kunt altijd elk stuk tussen twee knikpunten apart beschrijven, dus voor $x < -1$, $-1\le x < 0$, $0\le x < 1$, en $1\le x$. Dan krijg je iets als dit:
$$
f(x)=\begin{cases}
-x & x < -1\\
x+2 & -1\le x < 0\\
-x+2 & 0\le x < 1\\
x & 1\le x
\end{cases}
$$
Of je herkent twee absolute-waardefuncties:
$$
f(x)=\begin{cases}
|x+1|+1 & x \le0\\
|x-1|+1 & 0\le x
\end{cases}
$$
Of je ziet dat je iets kunt doen als in je vorige vraag: $f(x)=1+\bigl||x|-1\bigr|$.

De eerste methode, netjes alle intervallen langslopen, werkt altijd. Als je wat meer ervaring krijgt ga je vaker eenvoudigere formules zien.

©2004-2025 WisFaq