WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Afstandsbepaling op de aardbol

Dit is een reactie op vraag 54267

Dag Oscar, wij moeten voor school hetzelfde doen als hier. Alleen snappen we niet goed hoe het werkt. We denken dat we het juist doen maar de uitkomst klopt niet. We doen dit voor Santiago in Chili tot Sydney. Kan je ons hierbij helpen. Alvast bedankt
Jan-Willem
3de graad ASO - maandag 22 januari 2024

Antwoord

Hallo Jan-Willem,

Jammer dat je jouw berekeningen niet vermeldt, anders hadden we kunnen meedenken over waar jouw fouten dan zitten. Ik geef aan hoe je de berekening kunt uitvoeren volgens de methode van de vraag waarop je reageert.

Santiago en Sidney liggen (nagenoeg) op dezelfde breedtecirkel: afgekapt op hele graden is dit 33°. De straal r van deze breedtecirkel kan je berekenen door de aarde te bekijken vanaf een punt boven de evenaar, zie de figuur hieronder:

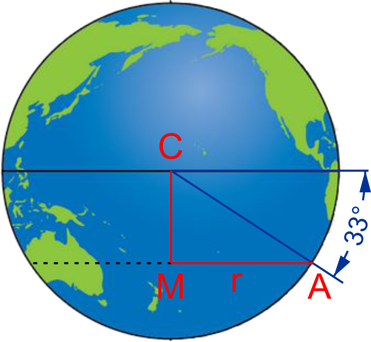
AC is de straal van de aarde, hoek A in driehoek AMC is de breedtegraad 33°, hiermee is de straal r van deze breedtegraad te berekenen.

Laten we dan de aarde eens bekijken vanaf een punt boven de zuidpool:

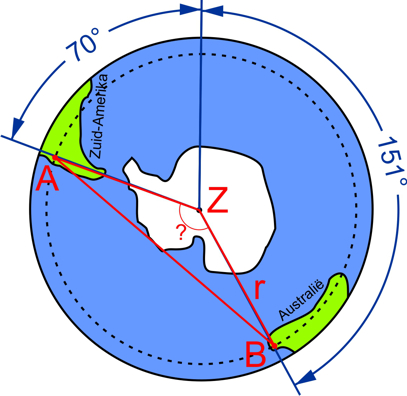
Z is de zuidpool, punt A geeft de ligging van Santiago aan, punt B de ligging van Sydney. De lengtegraden zijn ook aangegeven: 70° WL resp. 151° OL. Hiermee is hoek Z in driehoek AZB te berekenen. Omdat je de zijden ZA en ZB kent (de straal r van de breedtecirkel) kan je ook lijnstuk AB berekenen: de afstand tussen Santiago en Sydney, gemeten langs een rechte lijn dwars door de aarde heen.

Tot slot kijken we vanuit het middelpunt C van de aarde naar de punten A en B:

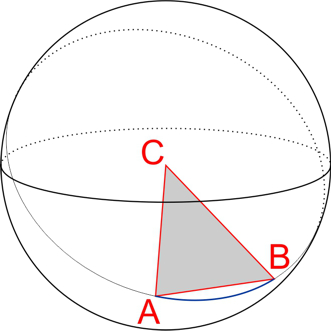
Van de driehoek ABC ken je alle zijden, dus je kunt hoek C berekenen. Wanneer je hoek C eenmaal hebt, bereken je de booglengte AB door te bedenken dat deze hoek C een deel van 360° is, de booglengte AB is datzelfde deel van de omtrek van de aarde.

Lukt het hiermee? Zo niet, stel dan gerust een vervolgvraag, maar geef dan wel aan waar het probleem ligt.

Overigens: het vraagstuk is ook op te lossen met behulp van boldriehoeksmeetkunde, kijk maar eens op Hoever is het van ... naar ...?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 23 januari 2024