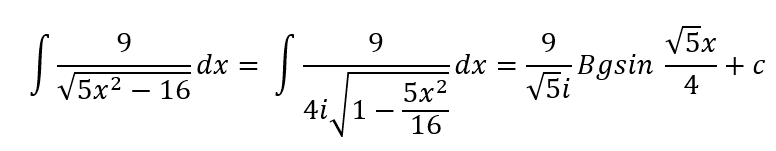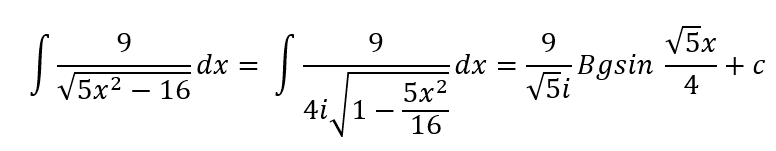
Ik begrijp dat de oplossing (9/wortel(5)) maal de ln van de absolute waarde van wortel(5) maal x + wortel (5x^2-16) is, maar zou de oplossing ook 9/(wortel(5) maal i) maal de Bgsin van (wortel(5) maal x / 4) kunnen zijn? Als je de wortel van -16 afsplitst in het begin krijg je 4i met i^2=-1 toch?
OPA
3de graad ASO - woensdag 10 mei 2023
Dat geeft problemen als je dit gebruikt om bepaalde integralen over reele intervallen uit te rekenen.
In
\int\frac{9}{\sqrt{5x^2-16}}\,\mathrm{d}x
hebben we het over x-en waarvoor 5x^2-16\ge0, en dus |x|\ge\frac{4}{\sqrt5}.
Maar in
\operatorname {Bgsin}\frac{\sqrt5 x}{4}
moet juist gelden dat |x|\le\frac{4}{\sqrt5}. Dat is vervelend. En dan hebben we het ook nog niet over de i in het antwoord; die maakt een reëel antwoord imaginair.
Overigens kan het wel; in de Complexe Analyse kun je \operatorname {Bgsin} in de logaritme uitdrukken:
\operatorname {Bgsin} z = \frac1i\log(iz+\sqrt{1-z^2})
maar daar moet je heel voorzichtig mee zijn want logaritmen en wortels hebben meer dan één waarde in het complexe vlak.