|
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||
|
\require{AMSmath}



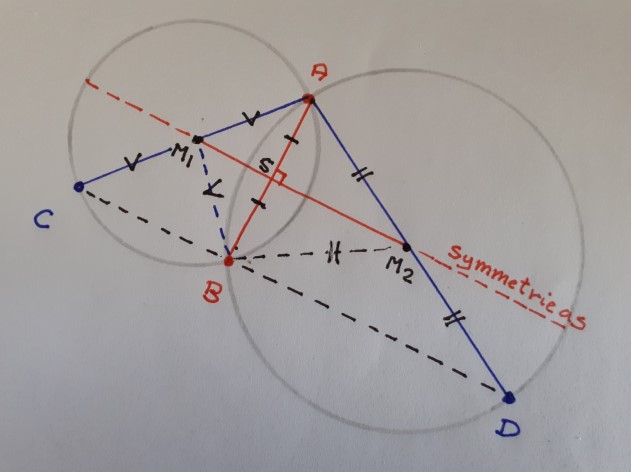
Bewijzen dat 3 punten collineair zijnTwee cirkels c1(M1,r1) en c2(M2,r2) snijden elkaar in de punten A en B. De middellijnen van c1 en c2 door A snijden c1 en c2 respectievelijk in de punten C en D. Bewijs dat de punten B, C en D collineair zijn. AntwoordDe lijn door M1 en M2 is symmetrieas van beide cirkels.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| |||||||||||||||||