WisFaq!

Bewijzen dat 3 punten collineair zijn

Twee cirkels c1(M1,r1) en c2(M2,r2) snijden elkaar in de punten A en B. De middellijnen van c1 en c2 door A snijden c1 en c2 respectievelijk in de punten C en D. Bewijs dat de punten B, C en D collineair zijn.

Ik ben tot een constructie gekomen, maar daar blijft het ook bij. Ik zie inderdaad dat de punten B, C en D collineair zijn, maar ik heb geen idee hoe ik dit kan bewijzen.

An
7-4-2023

Antwoord

De lijn door M1 en M2 is symmetrieas van beide cirkels.
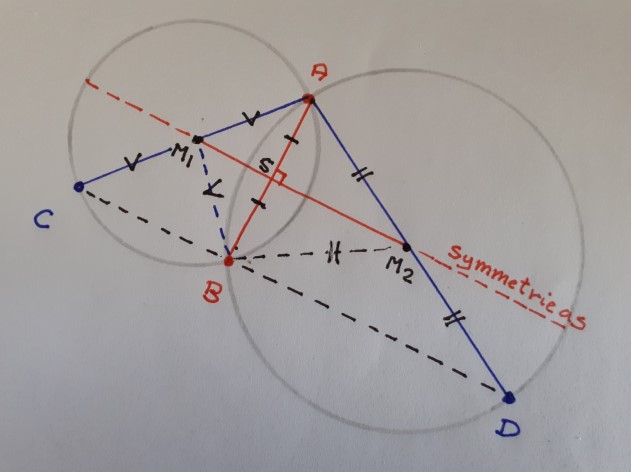
Deze lijn snijdt dus AB middendoor en ook loodrecht (spiegeling)
Nu zijn de driehoeken ASM₁ en ABC gelijkvormig
Omdat hoek ASM₁ = 90° is daarom ook hoek ABC = 90°
Op dezelfde manier is hoek ABD = 90°
En omdat deze hoeken samen 180° zijn liggen de punten C B en D op een lijn



Met vriendelijke groet
JaDeX

jadex
8-4-2023