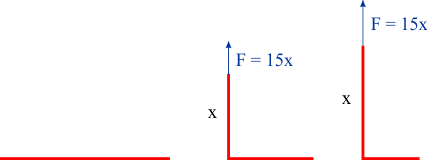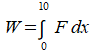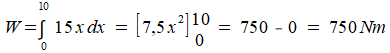WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Buigzame kabel

Dit is een reactie op vraag 92393

Hoe kan ik deze vraag oplossen met integralen?

A.B
3de graad ASO - zaterdag 12 juni 2021

Antwoord

Ik begrijp dat de kabel 15 meter lang is, en dat deze 10 meter wordt opgehesen. De kabel weegt 15 N per meter.

Onderstaande figuur laat de eenvoudigste manier zien om de verrichte arbeid te berekenen:

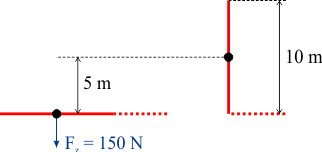
Links zie je de rode kabel op de grond liggen. Het rechter deel van 5 meter heb ik gestippeld, want dit blijft liggen en is voor de berekening niet relevant. De zwaartekracht op het linker deel van 10 meter is 10·15=150 N.

Wanneer het linker deel is opgehesen, dan is het zwaartepunt 5 meter omhoog gegaan, zie de rechter figuur. De hoeveelheid arbeid W die hiervoor nodig is, bereken je met:

Arbeid = kracht x afstand

W = 150·5 = 750 Nm.

Omdat de zwaartekracht op dit deel van de kabel constant is, heb je geen ingewikkelde integraal nodig.

Als je, als oefening, toch gebruik wilt maken van een integraal, dan gaat dit als volgt. In de figuur hieronder zie je hoe de kabel wordt opgehesen:

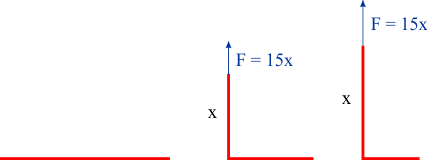
Als een lengte x is opgehesen, dan is de benodigde trekkracht 15x. Deze lengte x neemt toe van x=0 tot x=10. De trekkracht neemt dus ook toe. Voor de arbeid W geldt:

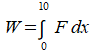
In dit geval:

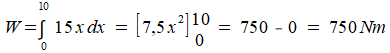
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 12 juni 2021