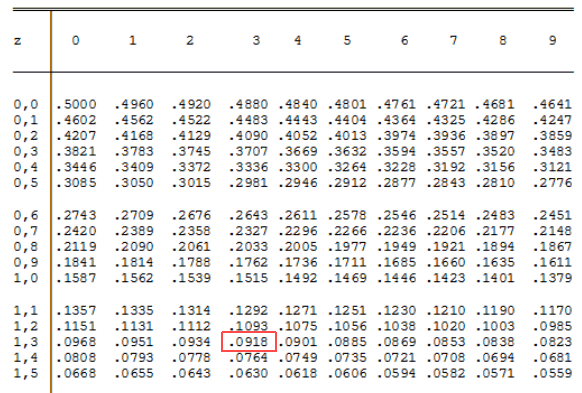WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Normale verdeling

Dit is een reactie op vraag 91611

Met de applet snap ik het. Alleen tijdens moet examens mag ik geen grafische rekenmachine gebruiken of een app zoals hier boven.

Het eerste deel van de formule snap ik. M/s = 56/4.5 = 0.091.

Maar het 2de deel. ? 4.5 / 0.91 = 49.45? Wordt dit zo bedoelt ?
Elijah
Leerling mbo - donderdag 25 februari 2021

Antwoord

Voor berekeningen zonder applet of GR gebruik je de standaard normale verdeling en een tabel. Ik neem aan dat je een tabel tot je beschikking hebt.

Bereken eerst de z-score:

$
\eqalign{z = {{50 - 56} \over {4,5}} \approx - 1,333}
$

Zoek in de tabel de waarde voor z=1,333.

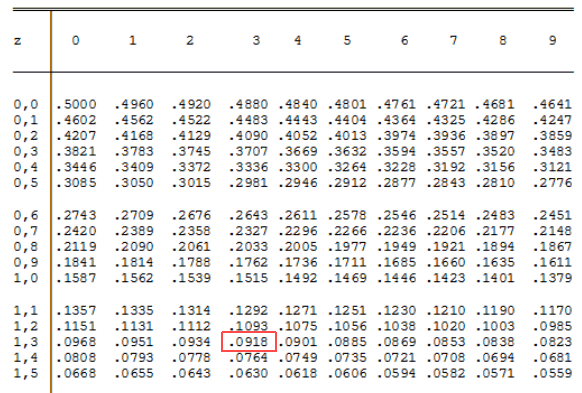
In de tabel staan alleen de waarden van de bovenste helft met de oppervlakte rechts van de gegeven $z$-waarde. Dat is allemaal niet zo'n probleem omdat de curve symmetrisch is.

P(x$>$1,333)=0,091 dus P(x$<$-1,333)=0,091
P(x$>$50)=0,909 oftewel ongeveer 91%.

Er is mee over te zeggen en er zitten hier en daar nog wat haken en ogen aan. Je kunt meer vinden over normale verdeling in de Lesbrief de normale verdeling

Zou dat lukken?

Naschrift
De waarde $
\phi (1,333) \approx 0,091
$ kan je berekenen door interpolatie.

$
\eqalign{
& \phi (1,33) = 0,0918 \cr
& \phi (1,34) = 0,0901 \cr
& \phi (1,333) = 0,0918 + 0,003 \cdot {{0,0901 - 0,0918} \over {1,34 - 1,33}} \cr
& \phi (1,333) \approx 0,091 \cr}
$

Wat dat betreft is een GR of een applet wel een stuk handiger.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 25 februari 2021