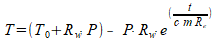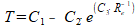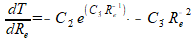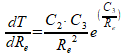WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Warmte koperdraad

Hoi,
Ik ben bezig om de weerstand van een koperdraad onder de motorkap van een auto te bepalen, echter loop ik vast bij de differentiaal vergelijk. De waarde Re is de relevante om het om het opgenomen vermogen te bepalen van de kabel door de motorwarmte.

Via:
P-(T-T0)/Rw =c·m·(dT/dt)

Kom ik uit op:
T=T0+Rw·P-P·Rw·e^(t/(c·m·Re))

Nu wil de e wegwerken, maar ik kom dan richting:
^d/_dReT= t₀+Rw·P-P·Rw·e^(^t/_c·m·Re)(^t/_c·m·Re)

Ik heb het idee dat in bovenstaand stuk de fout zit, maar ik weet niet precies hoe ik dit nu verder moet aanpakken.

Bij voorbaat dank voor de hulp
TDSAE
Student hbo - woensdag 9 december 2020

Antwoord

Je vraag is niet helemaal duidelijk, maar als ik het goed begrijp, wil je de (partiële) afgeleide van T naar Re weten in de formule:

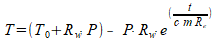
Voor het overzicht schrijf ik deze eenvoudiger:

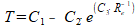
Hierin is:
C₁ = T₀+ R_w·P
C₂ = P·R_w
C₃ = ^t/_(c·m)

De afgeleide van de constante C₁ is 0. Zo vind ik:

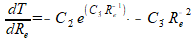
Iets overzichtelijker genoteerd:

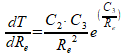
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 december 2020