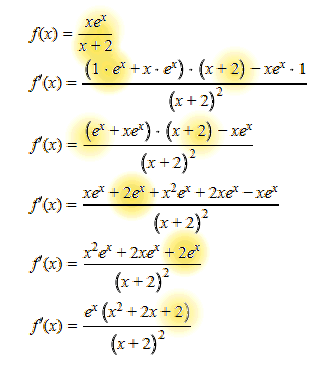WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentiëren

Gegeven:

f(x)=xe^x/(x+2)

Ik heb er een plaatje bij gezet voor de duidelijkheid. De uitkomst zou f'(x)=e^x(x²+2x+2)/(x+2)² moeten zijn, maar ik snap niet vanwaar die laatste 2 uit de teller komt?
melike
Student universiteit België - donderdag 15 oktober 2020

Antwoord

Kijk maar 's goed.

$
\eqalign{
& f(x) = {{xe^x } \over {x + 2}} \cr
& f'(x) = {{\left( {1 \cdot e^x + x \cdot e^x } \right) \cdot \left( {x + 2} \right) - xe^x \cdot 1} \over {\left( {x + 2} \right)^2 }} \cr
& f'(x) = {{\left( {e^x + xe^x } \right) \cdot \left( {x + 2} \right) - xe^x } \over {\left( {x + 2} \right)^2 }} \cr
& f'(x) = {{xe^x + 2e^x + x^2 e^x + 2xe^x - xe^x } \over {\left( {x + 2} \right)^2 }} \cr
& f'(x) = {{x^2 e^x + 2xe^x + 2e^x } \over {\left( {x + 2} \right)^2 }} \cr
& f'(x) = {{e^x \left( {x^2 + 2x + 2} \right)} \over {\left( {x + 2} \right)^2 }} \cr}
$

Er zit nog ergens een keer de productregel in. Vandaar misschien?

Naschrift

Waar komt die 2 vandaan?

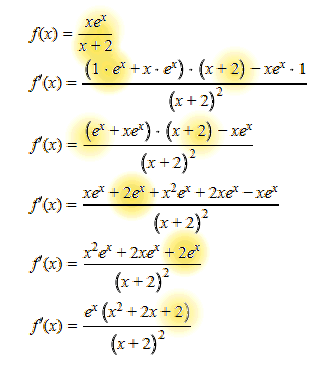
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 15 oktober 2020