|
|
|
\require{AMSmath}
Re: Re: Re: Re: Re: Extremumvraagstuk vuurpijl
Beste, ik heb een soortgelijke vraag maar met andere afmetingen. Ik kom echter nog steeds niet tot de juiste vergelijking om het op te lossen. Kan iemand de exacte vergelijking tonen om de minimale afstand te bepalen?
Alvast bedankt
Bert
Student universiteit België - zaterdag 29 augustus 2020
Antwoord
Hallo Bert,
Voor de baan van de vuurpijl geldt:
y = -1/90x2 + 4/3x + 20
De coördinaten van de top T van de boom zijn (50 , 30)
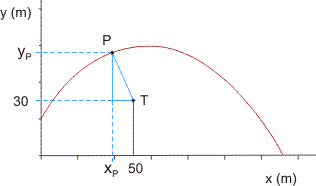
Voor de afstand PT geldt dan:
PT2 = (50-x)2 + (-1/90x2 + 4/3x -10)2
Wanneer je met bv. je grafische rekenmachine het minimum zoekt, dan vind je:
Minimum PT2 is 750,25... bij x=37,94...
De minimale afstand tussen vuurpijl en boom is dan √750,25... = 27,39... meter.
Je kunt ook eerst de afgeleide van PT2 bepalen:
d(PT2)/dx = -2(50-x) + 2(-1/90x2 + 4/3x -10)·(-2/90x + 4/3)
Wanneer je de haakjes wegwerkt, vind je een derdegraadsfunctie. Het zal niet de bedoeling zijn om het nulpunt exact uit te rekenen. Je kunt dan ook deze 'ruwe' vorm in je rekenmachine invoeren en het nulpunt bepalen. Je vindt dan dezelfde waarde voor x en daarmee dezelfde minimale afstand.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 29 augustus 2020
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 84487