WisFaq!

Re: Re: Re: Re: Re: Extremumvraagstuk vuurpijl

Beste, ik heb een soortgelijke vraag maar met andere afmetingen. Ik kom echter nog steeds niet tot de juiste vergelijking om het op te lossen. Kan iemand de exacte vergelijking tonen om de minimale afstand te bepalen?

Alvast bedankt

Bert
29-8-2020

Antwoord

Hallo Bert,

Voor de baan van de vuurpijl geldt:

y = -¹/₉₀x² + ⁴/₃x + 20

De coördinaten van de top T van de boom zijn (50 , 30)



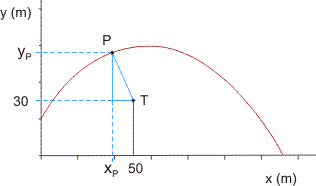
Voor de afstand PT geldt dan:

PT² = (50-x)² + (-¹/₉₀x² + ⁴/₃x -10)²

Wanneer je met bv. je grafische rekenmachine het minimum zoekt, dan vind je:

Minimum PT² is 750,25... bij x=37,94...
De minimale afstand tussen vuurpijl en boom is dan √750,25... = 27,39... meter.

Je kunt ook eerst de afgeleide van PT² bepalen:

^d(PT2)/_dx = -2(50-x) + 2(-¹/₉₀x² + ⁴/₃x -10)·(-²/₉₀x + ⁴/₃)

Wanneer je de haakjes wegwerkt, vind je een derdegraadsfunctie. Het zal niet de bedoeling zijn om het nulpunt exact uit te rekenen. Je kunt dan ook deze 'ruwe' vorm in je rekenmachine invoeren en het nulpunt bepalen. Je vindt dan dezelfde waarde voor x en daarmee dezelfde minimale afstand.

GHvD
29-8-2020