|
|
|
\require{AMSmath}



Standaarddeviatie
Hallo. Ik heb de oefenvragen gemaakt voor de standaarddeviatie met 1, 50, 51, 52, 53, 86 maar ik kom op een ander antwoord uit.
Zo berekende ik het:
tel bij elkaar op, deel door het aantal waardes: 48,83
Van elke waarde trek je 48,83 af en dan vermenigvuldig je die uitkomst met zichzelf. Dan kreeg ik:
1 $\to$ 2287,71
50 $\to$ 1,37
51 $\to$ 4,71
52 $\to$ 10,05
53 $\to$ 17,39
86 $\to$ 1381,61
Ik tel die bij elkaar op, deel door het aantal variabelen (6) en dan kom ik op 617,14.
Ik wortel dat en krijg 24,84.
Wat is er fout gegaan?
Groeten
Floris
Student hbo - donderdag 25 juni 2020
Antwoord
Als je de gegevens beschouwt als populatie dan klopt je berekening wel:
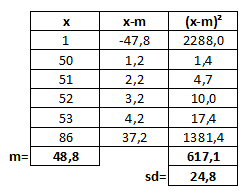
Als je dit beschouwt als steekproef dan moet je bij de standaardeviatie niet delen door $n$ maar door $n-1$. Je krijgt dan $
\sigma \approx {\text{27}}{\text{,2}}
$.
Het ging bij de oefening om Steekproef B dus je moet de SD hebben voor steekproeven. Helpt dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 25 juni 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










