|
|
|
\require{AMSmath}



Koekjes
In een fabriek worden koekjes gemaakt met een gemiddelde massa van 22 gram en een standaardafwijking van 4 gram. Een aantal koekjes wordt verpakt in een doos. Volgens de fabrikant is de gemiddelde massa van een koekje uit minstens 99% van de dozen minstens 20 gram. Hoeveel koekjes miet de fabrikant minstens in een doos steken?
hoe moet ik eraan beginnen?
het antwoord moet 22 zijn
Anna
3de graad ASO - woensdag 6 mei 2020
Antwoord
Hallo Anna,
Eerst: bedenk dat, wanneer de massa van koekjes normaal verdeeld is, dan is de gemiddelde massa van n koekjes ook normaal verdeeld. De standaardafwijking van de massa van 'losse' koekjes is 4 gram (\sigmax=4). Dan geldt voor de standaardafwijking \sigmax-gem van de gemiddelde massa van n koekjes:
\sigmax-gem = 4/√n
Dit noemt men wel de wortel-n-wet.
Maak bij dit soort vragen altijd een schets van de normaalverdeling om inzicht te krijgen in het vraagstuk. De gemiddelde massa van n koekjes is 22 gram. De spreiding moet zodanig zijn dat bij slechts 1% van de dozen de gemiddelde massa minder is dan 20 gram. De schets ziet er dan zo uit:
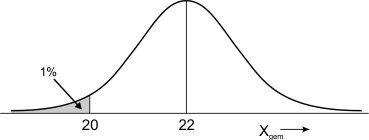
Bereken welke standaardafwijking hoort bij deze schets. Dit is dan \sigmax-gem, de standaardafwijking van de gemiddelde massa van n koekjes. Met de formule hierboven kan je dan de minimale waarde van n berekenen.
Opmerking: In de regel vind je geen geheel getal voor n. Rond altijd af naar boven, ook als het dichtstbijzijnde gehele getal lager ligt. Immers, als je naar beneden zou afronden, dan wordt \sigmax-gem iets te groot, met als gevolg dat iets meer dan 1% van de dozen te licht zal zijn.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 6 mei 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|










