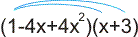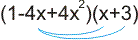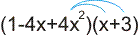WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Driedubbele haakjes

Hoe los je de volgende vergelijkingen op zonder haakjes?

Y = (1-2x)²(x+3)

en

Y = 3-x(x-6)²

alvast bedankt
Rose
Leerling bovenbouw havo-vwo - woensdag 13 september 2017

Antwoord

Hallo Rose,

Beide vergelijkingen hebben twee onbekenden, dan valt er niets op te lossen. Oplossen zou betekenen: de waarde van x en y berekenen. Maar met deze twee onbekenden mag je voor x kiezen wat je wilt, bij elke waarde van x kan je een bijbehorende waarde voor y berekenen.

Misschien bedoel je: hoe werk je de haakjes weg? Of bedoel je: los op: (1-2x)²(x+3)=0? Ik zal beide vragen bespreken.

Haakjes wegwerken:
Hiervoor bedenk je dat (1-2x)² betekent: (1-2x)(1-2x). De eerste vergelijking kan je dus schrijven als:

y = (1-2x)(1-2x)(x+3)

Dan werk je eerst één paar haakjes weg zoals je gewend bent, bijvoorbeeld het eerste paar. Je krijgt dan:

y = (1-4x+4x²)(x+3)

Dan combineer je op dezelfde manier elke term uit het eerste paar haakjes met elke term uit het tweede paar haakjes. Je krijgt dan als eerste:

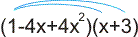
dus:

y = 1·x + 1·3 ....

Dan volgt:

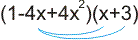
dus:

y = 1·x + 1·3 -4x·x -4x·3 ...

en tot slot:

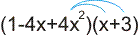
dus:

y = 1·x + 1·3 -4x·x -4x·3 + 4x²·x + 4x²·3

Nu even netter noteren:

y = x+3-4x²-12x+4x³+12x²

en gelijksoortige termen samenvoegen:

y = 4x³+8x²-11x+3

Dan: oplossen: (1-2x)²(x+3)=0
Ga niet automatisch haakjes wegwerken. Je krijgt dan een vergelijking met een 3^e macht, dat is lastig. In dit geval zijn haakjes juist handig want:

(1-2x)²(x+3)=0
als:
(1-2x)=0 of (x+3)=0

Je hebt één moeilijke opgave gesplitst in twee eenvoudige opgaven. De eerste levert:
1-2x=0
-2x=-1
x=¹/₂

De tweede:
x+3=0
x=-3

Dus de oplossing is:

x=-3 of x=¹/₂

Nu je tweede vergelijking:
Haakjes wegwerken gaat op dezelfde manier als hierboven. Probeer dit nu zelf.
Oplossen van 3-x(x-6)² is lastig: je kunt niet herleiden tot een vorm A·B=0 (zoals bij je eerste vergelijking). Je moet dus een 3^e-graad vergelijking oplossen. Wellicht ben je haakjes vergeten?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 13 september 2017