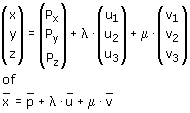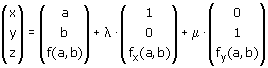WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Raakkruis en raakvlak

Beste

Ik ben (zelfstandig) aan het leren over afgeleiden van meerdere veranderlijken. Ik heb vernomen dat je met de partiële afgeleiden een raakkruis/raakvlak kunt bekomen?

Mijn vraag aan u: Wanneer bekom je deze? M.a.w. wanneer heb je een raakvlak en wanneer een raakkruis? En is het bekom je de formule voor beiden op dezelfde manier?

Hartelijk dank
Roland
Student universiteit België - dinsdag 6 juni 2017

Antwoord

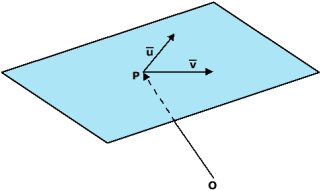In de ruimte kan je vlakken weergeven als vectorvoorstelling. Het vlak door P kan je met twee richtingsvectoren schrijven als:

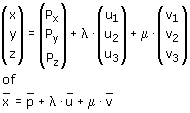
Als z=f(x,y) een raakvlak heeft in het punt P(a,b,f(a,b)) dan kan je een vectorvoorstelling van dat raakvlak zo vinden:

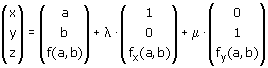
Je kunt deze vectorvoorstelling herleiden tot de volgende vergelijking:

z(x,y) = f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b)

Je hebt een `raakkruis' als de beide partiele afgeleiden bestaan; je hebt een raakvlak als de functie differentieerbaar is in dat punt.

Partiële afleidbaarheid

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 6 juni 2017